4

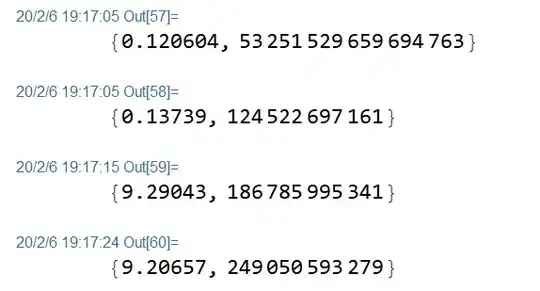
These four commands

ParallelSum[Prime[i]^2, {i, 1, 10000} ] // AbsoluteTiming
ParallelSum[Prime[i] + Prime[i + 1], {i, 1, 10000} ] // AbsoluteTiming
ParallelSum[ Prime[i] + Prime[i + 1] + Prime[i + 2], {i, 1,  10000} ] // 
AbsoluteTiming
ParallelSum[Prime[i] + Prime[i + 1] + Prime[i + 2] + Prime[i + 3], {i, 1, 
10000} ] // AbsoluteTiming

gives out nearly the same time.

but when I change 10000 to 100000

ParallelSum[Prime[i]^2, {i, 1, 100000} ] // AbsoluteTiming
ParallelSum[Prime[i] + Prime[i + 1], {i, 1, 100000} ] // AbsoluteTiming
ParallelSum[
Prime[i] + Prime[i + 1] + Prime[i + 2], {i, 1,  100000} ] // AbsoluteTiming
ParallelSum[Prime[i] + Prime[i + 1] + Prime[i + 2] + Prime[i + 3], {i, 1, 
100000} ] // AbsoluteTiming

enter image description here

what makes the difference?

Mr.Wizard
  • 271,378
  • 34
  • 587
  • 1,371
AsukaMinato
  • 9,758
  • 1
  • 14
  • 40
  • 1
    I guess that coupling ParalellSum and Prime is not especially constructive in order to understand the underlying issues. Prime is based on PrimePi which uses so called Lagaris Miller Odlyzko method finding primes. This is a sophisticated algorithm using sparse caching and sieving. You should perform extensive analysis for much larger numbers. There is yet another issue related to Prime which has quite different timings. You should carefully test this post What is so special about Prime? – Artes Feb 06 '20 at 12:07
  • 1
    Many parameters are automatically chosen in Parallel.... The argument might have a great influence on the parameters. I would suggest forcing as many parameters as possible to ensure a fair comparison. See e.g. https://mathematica.stackexchange.com/questions/55242/sudden-increase-in-timing-when-summing-over-250-entries/ – anderstood Feb 06 '20 at 13:53

1 Answers1

1

Are you interested in rapidly summing primes? or was that just an example to illustrate a ParallelSum question?

If you want fast methods for summing primes please see this question and its answers.

Please note that the following is a much faster way to sum the sequence of 4 adjacent primes, the fourth example in your question.

With[{m = 10000}, AbsoluteTiming[
   4*ParallelSum[Prime[i], {i, 1, m + 3}] -
              3*(Prime[1] + Prime[m + 3]) -
              2*(Prime[2] + Prime[m + 2]) -
                (Prime[3] + Prime[m + 1])
   ]]
KennyColnago
  • 15,209
  • 26
  • 62