When we try to evaluate Prime on big numbers (e.g. 10^13) we encounter the following issue:
Prime[10^13]
Prime::largp: Argument 10000000000000 in Prime[10000000000000] is too large for this implementation. >>Prime[10000000000000]
Following this message, we can read in the documentation that the largest supported argument in Prime is typically about $2^{42}$. With a kind of divide and conquer approach, we can figure out that the maximal argument of Prime is:
OmegaPrime = 7783516045221;
1. What determines this number ? A hardware/software and/or conceptual/mathematical issue or maybe an arbitrary system cut-off ?
The problem seems to be a bit more obscure, since one encounters something like this:
Prime @ {# + 1, #, # + 1} & @ OmegaPrime
Prime::largp: Argument 7783516045222 in Prime[7783516045222] is too large for this implementation. >>{ Prime[7783516045222], 249999997909357, 249999997909367}
(It takes more than two minutes to evaluate.)
An analog of OmegaPrime is OmegaPrimePi for PrimePi :
OmegaPrimePi = 25 10^13 -1;
I can find even bigger primes with Prime if I evaluate for example:
Select[Range[249999997909357, 25 10^13], PrimeQ] // Length
63142
Prime[ OmegaPrime + 63142]
250000000000043
However I cannot evaluate PrimePi for numbers greater than OmegaPrimePi. It appears that Prime has a dynamically extensible domain while PrimePi does not.
2. How do I detect this property in advance from the system ?
I mean not to play around with e.g. Select[Range[a,b], PrimeQ], but for example to read it from Attributes or anything else.
UPGRADE version 12.1
Domains of Prime as well as PrimePi have been significantly extended
and now
OmegaPrimePi = 2^63 - 1
9223372036854775807
It is a much larger domain than formerly:
OmegaPrimePi/(25 10^13 - 1) // N
36893.5
Now OmegaPrime is simply the value of PrimePi on OmegaPrimePi, namely
OmegaPrime = 216289611853439384;
and the domain of Prime is extensible as before, i.e. evaluating on the fresh kernel
Prime[OmegaPrime + 1]
Prime[216289611853439385]
Prime[OmegaPrime]
9223372036854775783
this took about $6$ minutes to evaluate on my computer.
Prime[OmegaPrime] is the gratest prime number below OmegaPrimePi.
Prime[OmegaPrime + 1]
9223372036854775837
Since version 12.1 PrimePi works with several algorithms which can be chosen with Method.
Answers by Andrzej Kozłowski and Daniel Lichtblau were both helpful, although they haven't explained the origin of OmegaPrime.
Now with the last upgrade this issue becomes clear.
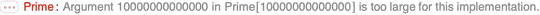
Primestag since M contains quite a good functionality in this field and there could appear many interesting and related questions. – Artes Mar 22 '12 at 00:48Attributesto answer such a question, as that function deals with various general-type properties. My guess is that the only possibility beyond experimentation is looking at the documentation. And if that doesn't help, ask Wolfram tech support. – murray Mar 22 '12 at 00:55Attributeshere only for instance of what one could expect since I had checked this before and it hadn't enlightened me more. – Artes Mar 22 '12 at 01:01PrimecallsPrimePimany (namely, 1,013,381) times when given an argument of yourOmegaPrime:nums = Reap[Internal`InheritedBlock[{PrimePi}, Unprotect[PrimePi]; pp:PrimePi[n_] /; (Sow[n]; True) := pp; Protect[PrimePi]; Prime[7783516045221]]][[2, 1]]; ListLogLogPlot[nums, MaxPlotPoints -> 1000, Joined -> True]gives nearly a straight line. What this means, if anything, I have no idea, but it shows at least some concrete relationship between the two functions. – Oleksandr R. Mar 22 '12 at 03:19Prime@PrimePi@Range[101, 105]returns 'Range[101, 105], i.e. identity, but notPrimePi@Prime`. There are also some issues of their internal implementations which are certainly more obscure. – Artes Mar 22 '12 at 09:11