I am trying to find the boundary points of some concave 3D region which is described by a list of points. If the region were convex I would take the convex hull and simply extract the coordinates there.
However, since the shape is concave I need to use some alternative algorithm. For example I can implement alpha shapes such as proposed in
DelaunayMesh in a specified closed region - creating a concave hull from a set of points
and
I can successfully obtain a MeshRegion object that portrays the shape I want. However, unlike the convex hull the required implementations such as a Delauney Triangulation or the code proposed in https://mathematica.stackexchange.com/a/88769/45020 produce a MeshRegion that still contains all points. It just selects which triangles to include however it keeps internal triangles. Thus, I cannot easily pick only those points that are at the boundary. I tried applying RegionBoundary which works for 2D shapes but when applied to the 3D mesh it acts as the identity for some reason.
Example data:
pts = Join[RandomPoint[Cuboid[{0, 0, 0}, {1, 1, 1}], 1000],
RandomPoint[Cuboid[{1, 0, 0}, {2, 0.5, 0.5}], 1000]];
I want to obtain only those points at the boundary of the shape (discarding points in the interior).
This question was based on a misunderstanding where I used a function alphashapes that was meant only for 2D. The issue is resolved by using the correct one given in How do I create a triangulated surface from points?. Using this the simple way given by Carl Lange in the comments works.
(Perhaps I will delete this question since it came down to a trivial mistake.)
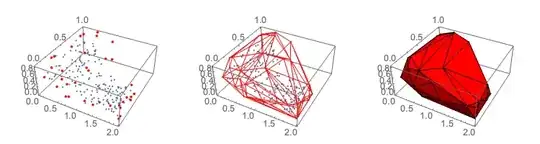
RegionBoundary@alphaShapes[pts, .3]and the shape looks very good to me. Then you could use MeshCoordinates on the resulting shape. – Carl Lange Feb 14 '20 at 16:45