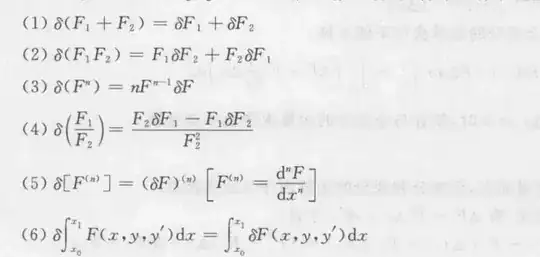The functional is : $$J(y)=y^{2}(x_{0})+\int_{x_{0}}^{x_{1}}(xy+y'^{2}) dx$$ In the textbook, the result of finding the functional variation according to the functional variation defined by Lagrange is :
The variation sign δ has the following basic operational properties :
How to use MMA to define a correlation function and find the variation of this function according to the definition of Lagrange?