I see this variational problem here.
The functional is : $$J(y)=y^{2}(x_{0})+\int_{x_{0}}^{x_{1}}(xy+y'^{2}) dx$$ In the textbook, the result of finding the functional variation according to the functional variation defined by Lagrange is :
The variation sign δ has the following basic operational properties :
How to use MMA to define a correlation function and find the variation of this function according to the definition of Lagrange?
I really want to solve this problem, but when I replace y with y+ε*δ, it can't be expanded linearly, so I can't do further calculation.
f[x] /. f :> f + ε*δ
f'[x] + f[x] /. f :> f + ε*δ
I want to get the following result according to the linear operation rule of variation mentioned above:
f[x] + ε*δ f[x]
(f'[x] + ε*δ f'[x]) + (f[x] + ε*δ f[x])
But the above code cannot be expanded obviously. Please help me.
The title of the book is 《变分法基础》, the author is 老大中. And the relevant content is on page 59 to page 63.
You can get a photocopy of this book from here. The password of the online disk is wthj.

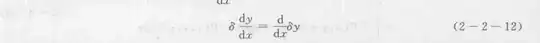


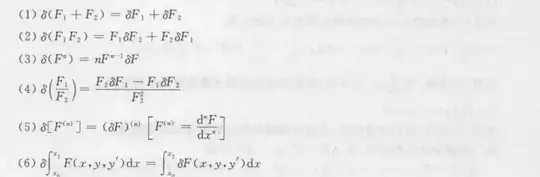

EulerEquations? – AccidentalFourierTransform Feb 21 '20 at 03:03VariationalMethodsfunction package, but I want to do a similar custom function to solve variational problem according to the textbook definition. – A little mouse on the pampas Feb 21 '20 at 03:07