0

Because of the need of the operation rules of variational notation, I want to achieve the following effects:

Through[(f + s)'[x]]
Through[(f + s)''[x]]

I want to get the following results:

f'[x] + s'[x]
f''[x] + s''[x]

I need a general and easy way to achieve the above requirements. What should I do?

As mentioned below, LouisB's method can be used to solve the problem of single replacement, but how to realize the whole replacement for complex formula?

y[x0] + y[x] + y'[x] + x*y''[x]

I want to replace the function header y with y + εδy to get something like this:

y[x0] + ε*δ[y[x0]] + 
 y[x] + ε*δ[y[x]] + 
 y'[x] + ε*δ[y'[x]] + 
 x (y''[x] + ε*δ[y''[x]])

In addition, for the following cases:

replaceHead = # /. 
    h : (y | 
        Derivative[_][y]) :> (Times[ε, δ@
         h[#]] &) &;
expr = (y[x0]^2) + Integrate[x y[x] + D[y[x], x]^2, {x, x0, x1}];
expr + replaceHead@expr

I need the results like this:

2 y[x0] δ[y[x0]] + 
 Integrate[(x δ[y[x]] + 
    2 Derivative[1][y][x] δ'[y[x]]), {x, x0, x1}]

But kglr's method can't combine integrals to get the form I want.

A little mouse on the pampas
  • 5,760
  • 2
  • 13
  • 40
  • 5
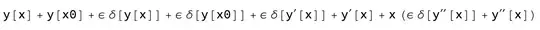
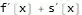
    Through[Distribute[(f + s)'][x]] and Through[Distribute[(f + s)''][x]] – LouisB Feb 21 '20 at 07:34
  • @LouisB Thank you very much for your help. I have updated my question. Can you spare time to solve it? – A little mouse on the pampas Feb 21 '20 at 09:28
  • 1
    PleaseCorrectGrammarMistakes, it is impossible to follow how your requirements in the two updates are related to the previous one. Your first update says a term like x y[x] is should become x (y[x] + ε*δ[y[x]]), you second says it should become x δ[y[x]]. What happened to ε between your first update and the second? – kglr Feb 23 '20 at 00:28
  • @kglr In fact, my goal in updating the problem is to solve this problem finally. It's better to answer this question directly. – A little mouse on the pampas Feb 23 '20 at 00:37

3 Answers3

2

If you don't insist on using Through, this is probably what you are looking for.

y[x0] + y[x] + y'[x] + x*y''[x];
% /. {Derivative[n_][y_][x_] :>  Derivative[n][y][x] + ϵ δ[Derivative[n][y][x]], 
      y_[x_] :>  y[x] + ϵ δ[y[x]]}

enter image description here

or to make it shorter

y[x0] + y[x] + y'[x] + x*y''[x];
% /. expr : Derivative[_][_][_] | _[_] :> expr + ϵ δ[expr]
Suba Thomas
  • 8,716
  • 1
  • 17
  • 32
1

Will this work for you?

 Plus @@ D[Through[{f, s}[x]], x]

Mathematica graphics

Plus @@ D[Through[{f, s}[x]], {x, 2}]

Mathematica graphics

Nasser
  • 143,286
  • 11
  • 154
  • 359
  • 1
    Thank you very much, but I need to replace all the f ''[x] in the formula with (f + δ)'' [x] when I do the variational operation, so your method can't meet my operation requirements. – A little mouse on the pampas Feb 21 '20 at 07:00
1
ClearAll[replaceHead]
replaceHead = # /. h : (y | Derivative[_][y]) :> (Times[ε, δ @ h[#]] &) &;

Example:

expr = y[x0] + y[x] + y'[x] + x*y''[x];

desired = y[x0] + ε*δ[y[x0]] + y[x] + ε*δ[y[x]] + y'[x] + ε*δ[y'[x]] + x (y''[x] + ε*δ[y''[x]]);

res = expr + replaceHead @ expr;

res == Simplify[desired]

True

TeXForm @ res

$\varepsilon x \delta \left(y''(x)\right)+x y''(x)+\varepsilon \delta \left(y'(x)\right)+y'(x)+\varepsilon \delta (y(x))+y(x)+\varepsilon \delta (y(\text{x0}))+y(\text{x0})$

kglr
  • 394,356
  • 18
  • 477
  • 896
  • 1
    Thank you very much. I've updated the question. Your method can't combine integrals to get the result form I want. I hope you can modify it again. – A little mouse on the pampas Feb 21 '20 at 23:14
  • After executing your code for the expression expr = (y[x0]^2) + Integrate[x y[x] + D[y[x], x]^2, {x, x0, x1}], the result is Integrate[(ε^2 δ[ Derivative[1][y][x]]^2 + ε x δ[y[x]]), {x, x0, x1}] + Integrate[(Derivative[1][y][x]^2 + x y[x]), {x, x0, x1}] + ε^2 δ[y[x0]]^2 + y[x0]^2 , while the result of the textbook is 2 y[x0] δ[y[x0]] + Integrate[(2 Derivative[1][y][x] Derivative[1][δ][y[x]] + x δ[y[x]]) , {x, x0, x1}]. How to modify it? – A little mouse on the pampas Feb 22 '20 at 07:45
  • 1
    @PleaseCorrectGrammarMistakes, this answer is meant to solve the question posed in your previous edit (for expressions like y[x0] + y[x] + y'[x] + x*y''[x]). Naturally, it will not work for arbitrary input expression. – kglr Feb 22 '20 at 23:25
  • Thank you very much, but how to find a general solution to solve this problem? – A little mouse on the pampas Feb 23 '20 at 00:10