Making cool animations of an accretion disk/planetary disk

Question

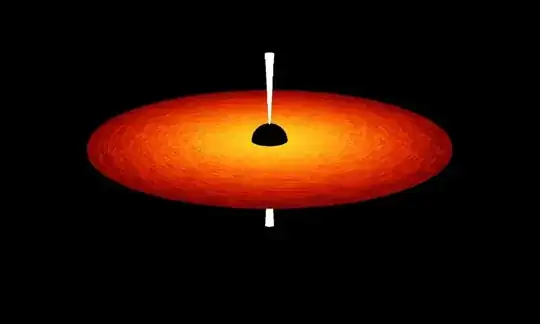
I am trying to make an animation of an accretion disk or a planetary disk. For example, a cool disk showing below (created by NAHKS TR'EHNL): or in this link

Here is what I have tried so far:

step1：Set the inner boundary rmin and the outer boundary rmax of the disk:

{rmin, rmax} = {0.1, 1.0};

Step 2: Define a function that gives the temperature gradient of the disk:

temgrad[r_] := (r - rmin)/(rmax - rmin)

You can see that the function =0 at the inner boundary and =1 at the outer boundary of the disk. The function will be used to color code the disk.

Step 3 Making a parametric plot of the disk, rendering the disk by using the ColorFunction:

figdisk = ParametricPlot3D[{r Cos[\[Theta]], r Sin[\[Theta]], 0}, {r, rmin, rmax}, {\[Theta], 0, 2 \[Pi]}, PlotPoints -> 100, Mesh -> False, Axes -> False, Boxed -> False, BoundaryStyle -> Opacity[0], Lighting -> {{"Ambient", White}}, Background ->Black, ColorFunctionScaling -> False, ImageSize -> {500, 300}, ColorFunction -> (ColorData[{"SolarColors", "Reverse"}][temgrad[Sqrt[#1^2 + #2^2]]+ 0.1 RandomReal[{-1, 1}]] &)];

The trick here in ColorFunction is that random values are assigned and added to the original temperature gradient, so to mimic the random fluctuations.

For the black hole, I use a simple sphere:

figBH = Graphics3D[{Black, Sphere[{0, 0, 0}, rmin]}];

for the jets I use cones (point to the top as well as the bottom):

figjet = Show@MapThread[ParametricPlot3D[{0.05 z Cos[t], 0.05 z Sin[t], z}, {z, #1, #2}, {t, 0, 2 \[Pi]}, Mesh -> False, PlotStyle -> Glow[Blend[{White, Lighter@Blue}]]] &, {{-5 rmin, rmin}, {-rmin, 5 rmin}}];

Then combining these figures presents my toy accretion disk：

Show[figdisk, figBH, figjet]

Now the problems are:

1. The appearance of the example disk seems to be natural as given at the top of this post. It is more like a real flow with fluctuations and even some random magnetic field lines on it.
2. Same for the jet, the example's jet is more realistic with fluid-like materials ejected outward while mine jet..... I have seen this post that simulated realistic jet engine flame, but it does not look like the fragmented thing in the example.

3. The way I choose to plot the disk only gives a surface (or a disk without thickness), which is not true in nature. The disk should have some thickness (varying with the radius).

   Can anyone help me to improve this piece of art? Thank you so much in advance!

Update_20200228

MassDefect suggested that a z-component can be added to make an ellipsoidal shape. And here is what I came up:

figdisk = ParametricPlot3D[{{r Cos[\[Theta]], r Sin[\[Theta]], .5 (r - rmin) Sqrt[rmax^2 - r^2]}, {r Cos[\[Theta]], r Sin[\[Theta]], -.5 (r - rmin)*Sqrt[rmax^2 - r^2]}}, {r, rmin, rmax}, {\[Theta], 0,(*2 *)\[Pi]}, PlotPoints -> 100, Mesh -> False, Axes -> False, Boxed -> False, BoundaryStyle -> Opacity[0], Lighting -> {{"Ambient", White}}, Background ->(*White*)Black, ColorFunctionScaling -> False, ImageSize -> {300, 300}, ColorFunction -> (ColorData[{"SolarColors", "Reverse"}][temgrad[Sqrt[#1^2 + #2^2]] + 0.1 RandomReal[{-1, 1}]] &)];

Now only half of the disk is plotted to show the cross section:

For the problem of creating a more fluid-like one, I found the algorithm for procedural terrain or Perlin noise (invented by Perlin in 1983) might help. This post made really nice gas animations.