Why do the Integrate and NIntegrate give different results?

Question

Bug introduced in 12.0 or earlier and persisting through 12.0.0 or later

I'm using Mathematica to calculate the following integral, but I don't know why the result of using Integrate function contains complex number:

Integrate[Sqrt[1/(2*9.8*(Sin[Pi/3] - Sin[θ]))], {θ, ArcSin[2./3 Sin[Pi/3]], Pi/3.}]
 (* 0.398283 + 0.510508 I *)

NIntegrate[Sqrt[1/(2*9.8*(Sin[Pi/3] - Sin[θ]))], {θ, ArcSin[2./3 Sin[Pi/3]], Pi/3.}]
(* 0.398283 *)

I'd like to know why the two output results are different and why the first result contains a complex number.

Making use of exact numbers, one obtains the result of Integrate[ Sqrt[1/(298/10(Sin[Pi/3] - Sin[[Theta]]))], {[Theta], ArcSin[2/3 Sin[Pi/3]], Pi/3}] as $$\frac{1}{7} i \sqrt{5} \left(\frac{2 F\left(\frac{1}{4} \left(\pi -2 \cot ^{-1}\left(\sqrt{2}\right)\right)|4 \left(\sqrt{3}+2\right)\right)}{\sqrt{2-\sqrt{3}}}-K\left(\frac{1}{4 \sqrt{3}+8}\right)\right) $$. This explains a small imaginary part as a round-off error. — user64494, Mar 03 '20 at 07:32
Also try Integrate[ Sqrt[1/(29.80000000000000000000000(Sin[Pi/3] - Sin[[Theta]]))], {[Theta], ArcSin[2.0000000000000000000/3 Sin[Pi/3]], Pi/3.00000000000000000}] to increase the working precision. Don't hesitate to ask for further explanation in need. — user64494, Mar 03 '20 at 16:36
You guys closed it too soon. Integrate[integrand, {\[Theta], ArcSin[2/3 Sin[Pi/3.]], Pi/3}] gives you 0.398283 + 0.510508 I, which is a significant difference from the other answers, but wouldn't be expected to differ. The upper bound of the integral is singular, and causes problems. — MikeY, Mar 03 '20 at 16:51
@user64494, take a look at the edited answer. It's actually an interesting subtlety at work. — MikeY, Mar 03 '20 at 17:00
@user64494, it surprised me that if I set for the bounds {θ, ArcSin[2./3 Sin[Pi/3]], Pi/3} with an exact upper bound but numerical lower, that I get a significantly different answer from exact upper and lower bounds of {θ, ArcSin[2/3 Sin[Pi/3]], Pi/3}, and the imaginary part is not round-off error. It's just the wrong answer. — MikeY, Mar 03 '20 at 17:19
@MikeY: The term 2./3 switches Integrate to NIntegrate with a small working precision and that leads to a non-exact result with a big error. One should use 2/3 or 2.00000000000/3 to obtain a correct result. — user64494, Mar 03 '20 at 17:37
@user64494 it must not be cleanly switching directly to NIntegrate, because it gives a significantly different answer from NIntegrate with the exact same bounds. — MikeY, Mar 03 '20 at 17:47
@MikeY: As written above, the term 2./3 switches Integrate to NIntegrate with a small working precision and that leads to a non-exact result with a big error. Be careful when reading comments. — user64494, Mar 03 '20 at 18:11
@user64494, your statement that a numeric bound in Integrate switches it to NIntegrate with a small(er?) working precision...I've never seen that written anywhere in the MMa documentation or in any answer here. Do you have a link? — MikeY, Mar 03 '20 at 18:26
@MikeY: [CASE:4389492] where a suggestion to include that in the documentation was reported by me. — user64494, Mar 03 '20 at 18:31
@MikeY The issue in the integral arises from taking the limits of the antiderivative at the end points, the approximate Limit[-2*EllipticF[(Pi - 2*θ)/4, 4*(2 + Sqrt[3])]* Sqrt[(Sqrt[3] - 2*Sin[θ])^(-1)]* Sqrt[(Sqrt[3] - 2*Sin[θ])/(-2 + Sqrt[3])], θ -> 1.0471975511965974, Direction -> 1, Assumptions -> True] versus the exact Limit[-2*EllipticF[(Pi - 2*θ)/4, 4*(2 + Sqrt[3])]* Sqrt[(Sqrt[3] - 2*Sin[θ])^(-1)]* Sqrt[(Sqrt[3] - 2*Sin[θ])/(-2 + Sqrt[3])], θ -> Pi/3, Direction -> 1, Assumptions -> True] // N -- I think it's probably round-off leading to a wrong branch. — Michael E2, Mar 03 '20 at 18:44
I know what I'd do if it was my integral. But I also learned something from digging into it that I hadn't learned from other Integrate != NIntegrate questions. And none of "trivial syntax error, incorrect capitalization, spelling mistake, or other typographical error and is unlikely to help any future visitors, or else it is easily found in the documentation." seemed to apply, and it was definitely an MMA question. Hope @GrammarMistakes got something out of it too! — MikeY, Mar 03 '20 at 18:57
@Micael E2: Integrate[Sqrt[1/(298/10(Sin[Pi/3] - Sin[\ [Theta]]))], \ [Theta]] $$\frac{1}{7} (-2) \sqrt{5} \sqrt{\frac{1}{\sqrt{3}-2 \sin (\theta )}} \sqrt{\frac{\sqrt{3}-2 \sin (\theta )}{\sqrt{3}-2}} F\left(\frac{1}{4} (\pi -2 \theta )|4 \left(\sqrt{3}+2\right)\right) $$ but Integrate[ Sqrt[1/(298/10(Sin[Pi/3] - Sin[\ [Theta]]))], {\ [Theta], ArcSin[2/3 Sin[Pi/3]], Pi/3}] $$\frac{1}{7} i \sqrt{5} \left(\frac{2 F\left(\frac{1}{4} \left(\pi -2 \cot ^{-1}\left(\sqrt{2}\right)\right)|4 \left(\sqrt{3}+2\right)\right)}{\sqrt{2-\sqrt{3}}}-K\left(\frac{1}{4 \sqrt{3}+8}\right)\right) $$. — user64494, Mar 03 '20 at 19:13
@Micael E2: Also the plots j = Integrate[Sqrt[1/(298/10(Sin[Pi/3] - Sin[\ [Theta]]))], \ [Theta]]; Plot[{Re[j], Im[j]}, {\ [Theta], ArcSin[2/3 Sin[Pi/3]], Pi/3}] do not show any discontinuities and branches. — user64494, Mar 03 '20 at 19:22
An example of the same issue in an answer to this question Why does Integrate declare a convergent integral divergent?. The explanation goes along the same way. — Artes, Mar 03 '20 at 19:43
@MikeY The main point is that feeding inexact input to an exact solver may produce incorrect results (GIGO). I don't think there's anything else to learn here about Mma. The exact solver fails, as usual when it does, because of a picayune, hidden, internal rounding error that led to something unpredictible. Speaking of unpredictible, consider Integrate[ Sqrt[1/(2*98/10*(Sin[Pi/3] - Sin[θ]))], {θ, ArcSin[2./3 Sin[Pi/3]], 1., Pi/3.}] — Michael E2, Mar 03 '20 at 19:50
Related: https://mathematica.stackexchange.com/questions/143722/bug-in-integral-related-to-beta-distribution#comment386573_143722, https://mathematica.stackexchange.com/questions/80637/strange-results-from-evaluating-a-simple-integral/80668#comment218417_80637, https://mathematica.stackexchange.com/q/72168/4999 — Michael E2, Mar 03 '20 at 20:44
Also: https://mathematica.stackexchange.com/q/127510/4999. Possible duplicate: Understand the difference between exact and approximate (Real) numbers (esp. last paragraph) — Michael E2, Mar 03 '20 at 20:50
seems fixed in MMA 12.1. I got 0.39828271593441 - 6.27615509572822*10^-9 I for Integrate and 0.398282728649972 for NIntegrate — user58955, Apr 11 '20 at 15:38

Michael E2 · Accepted Answer · 2020-03-05T12:37:01.190

Introduction and summary

The main point is that feeding inexact input to an exact solver may produce incorrect results. This should be more generally known. It is discussed in the last paragraph of this answer, Understand the difference between exact and approximate (Real) numbers.

A secondary point is that there is a bug in Limit[] (imo). The problem is extremely localized, but maybe it is worth exposing. The exact reasons for it and the extent of its generality are unclear. It can be avoided by using exact or arbitrary-precision input, so the main point above undermines its importance as a bug. In connection with the main point, it is worth pointing out that the Solve/Reduce suite of solvers take a different approach. They rationalize the input and numericize the output, emitting a warning message along the way. The same approach would work on this example. It may be worth considering whether Limit, Integrate and others might benefit from such an approach.

My original guess was that rounding error led to an unpredictable choice, probably choosing the wrong branch. I'm pretty sure now that it is not a wrong branch being chosen. There is a discontinuity at Pi/3, but the result does not correspond to choosing the wrong branch, AFAICT. Instead, I believe I have localized the problem to Limit failing to find the limit at a single machine floating-point number near Pi/3. This may or may not be due to a rounding error; for instance, if arbitrary-precision reals are used, Limit succeeds, and one of the principal effects of arbitrary-precision is to reduce rounding error, especially with respect to quantities canceling or testing equal. If it is rounding error, it's a hidden, internal error, which might be dismissed by referring to the main point.

On the other hand, since there is not such a problem at other floating point numbers near Pi/3, including Pi/3. itself, the user point of view should be to label this a bug and report it to WRI, the main point notwithstanding.

Analyzing the problem

A trace will reveal several limits, some of which test convergence, some which are used to apply the Fundamental Theorem of Calculus, and some which seem to test for branch cuts or other discontinuities.

Trace[
  Integrate[
   Sqrt[1/(2*98/10*(Sin[Pi/3] - Sin[θ]))], {θ, 
    ArcSin[2/3 Sin[Pi/3]], Pi/3.}],
  _Limit,
  TraceInternal -> True
  ] // Flatten

Below we show the last four and rewrite them in terms of the antiderivative used by Integrate internally (which has been stripped of a constant factor to be an antiderivative for the given integral), which I call ff[]. The first two limits evaluate ff[] at (or near) the end points of the interval of integration. The last two seem to be checking the antiderivative at the limit of integration for a branch discontinuity.

ff[θ_] := -2 EllipticF[1/4 (π - 2 θ), 4 (2 + Sqrt[3])] *
   Sqrt[1/(Sqrt[3] - 2 Sin[θ])] *
   Sqrt[(Sqrt[3] - 2 Sin[θ])/(-2 + Sqrt[3])];

{Limit[ff[θ], θ -> 1.0471975511965974, Analytic -> False, 
  Assumptions -> True, Direction -> 1, Method -> "InternalClassic"], 
 Limit[ff[θ], θ -> 0.6154797086703874, Analytic -> False, 
  Assumptions -> True, Direction -> -1, Method -> "InternalClassic"], 
 Limit[ff[θ], θ -> 1.0471975511965976, Analytic -> False, 
  Assumptions -> True, Direction -> -1, Method -> "InternalClassic"], 
 Limit[ff[θ], θ -> 1.0471975511965976, Analytic -> False, 
  Assumptions -> True, Direction -> 1, Method -> "InternalClassic"]}
(*
  {0.,
   -1.24682 - 1.59814 I,
   -2.39469*10^-8 - 1.59814 I,
   -2.39469*10^-8 - 1.59814 I}
*)

If we look at the limits of ff[] at consecutive floating-point numbers near the limit of integration, we see there is some misbehavior at θ -> 1.0471975511965974, which is equal to Pi/3. - $MachineEpsilon. This incorrect limit is what leads to the incorrect integral. There is also trouble with the limit at the number just below it also in one of the one-sided limits, but otherwise there is no problem with limits at other nearby numbers.

Limit[ff[θ], θ -> 1.0471975511965974 - 2 $MachineEpsilon]
{Limit[ff[θ], θ -> 1.0471975511965974 - $MachineEpsilon, Direction -> 1],
 Limit[ff[θ], θ -> 1.0471975511965974 - $MachineEpsilon, Direction -> -1]} ->
   Limit[ff[θ], θ -> 1.0471975511965974 - $MachineEpsilon]
Limit[ff[θ], θ -> 1.0471975511965974]
Limit[ff[θ], θ -> 1.0471975511965974 + $MachineEpsilon]
Limit[ff[θ], θ -> 1.0471975511965974 + 2 $MachineEpsilon]
(*
  -5.86663*10^-8 - 1.59814 I
  {0., -4.65708*10^-8 - 1.59814 I} -> Indeterminate
  0.
  -2.39469*10^-8 - 1.59814 I
  0. - 1.59814 I
*)

One might wonder if there is an evaluation problem near Pi/3. There does not seem to be one:

ff[θ] /. θ -> 1.0471975511965974 - 2 $MachineEpsilon
ff[θ] /. θ -> 1.0471975511965974 - $MachineEpsilon
ff[θ] /. θ -> 1.0471975511965974
ff[θ] /. θ -> 1.0471975511965974 + $MachineEpsilon (* == Pi/3. *)
ff[θ] /. θ -> 1.0471975511965974 + 2 $MachineEpsilon
(*
  -5.56222*10^-8 - 1.59814 I
  -4.62805*10^-8 - 1.59814 I
  -3.44954*10^-8 - 1.59814 I
  Indeterminate                    <-- θ -> Pi/3.
  -5.94877*10^-16 - 1.59814 I
*)

The Indeterminate result comes from Sqrt[3]-2 Sin[θ] evaluating to zero at Pi/3..

An irrelevant point: The round-off error in Sqrt[3]-2 Sin[θ] for θ around Pi/3. is nearly catastrophic in itself, and arbitrary-precision numbers lose about 16 digits of precision. However, since we multiply and divide by the same thing, (the square-root of) this quantity, the rounding error cancels out, and the results are much more accurate than they appear.

ff[θ] /. θ -> 1.0471975511965974`24 - 2*2^-52
ff[θ] /. θ -> 1.0471975511965974`24 - 2^-52
ff[θ] /. θ -> 1.0471975511965974`24
ff[θ] /. θ -> 1.0471975511965974`24 + 2^-52
ff[θ] /. θ -> 1.0471975511965974`24 + 2*2^-52
(*
  -5.622254*10^-8 - 1.59814200 I
  -4.767384*10^-8 - 1.59814200 I
  -3.72104*10^-8 - 1.59814200 I
  -2.22809*10^-8 - 1.5981420 I
  0.*10^-14 - 1.5981420 I
*)

Discontinuity

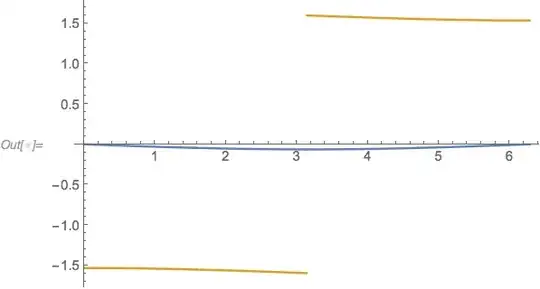
The discontinuity alluded to above occurs in the complex plane. It's conceivable that the problem relates to it, but it is unclear how exactly. Here is a plot of the real and imaginary parts of ff[] along a small path encircling the point where Limit fails:

Plot[
 ReIm[ff[θ]] /. θ -> 
    Rationalize[1.0471975511965974, 0] + 0.001 Exp[I t] // Evaluate,
 {t, 0, 2 Pi}]

Workarounds

For the limit:

N@Limit[ff[θ], θ -> Rationalize[1.0471975511965974`, 0]]
(*  -3.44954*10^-8 - 1.59814 I  *)

N@Limit[ff[θ], θ -> 1.0471975511965974`16]
(*  -3.54651*10^-8 - 1.59814 I  *)

Limit[Simplify[ff[θ], Sqrt[3] - 2 Sin[θ] > 0],
 θ -> 1.0471975511965974]
(*  -3.44954*10^-8 - 1.59814 I  *)

For the integral:

N@Integrate[Sqrt[1/(2*98/10*(Sin[Pi/3] - Sin[θ]))],
 {θ, ArcSin[2/3 Sin[Pi/3]], Pi/3}]
(*  0.398283 - 1.41859*10^-16 I  *)

N@Integrate[Sqrt[1/(2*98/10*(Sin[Pi/3] - Sin[θ]))],
 {θ, ArcSin[2/3 Sin[Pi/3]], Pi/3.`16}]
(*  0.398283 + 0. I  *)

Integrate[Sqrt[1/(2*98/10*(Sin[Pi/3] - Sin[θ]))],
 {θ, ArcSin[2/3 Sin[Pi/3]], Pi/3.}, Assumptions -> Sin[Pi/3] - Sin[θ] > 0]
(*  0.398283 - 2.83718*10^-16 I  *)

Integrate[Sqrt[1/(2*98/10*(Sin[Pi/3] - Sin[θ]))],
 {θ, ArcSin[2/3 Sin[Pi/3]], 1., Pi/3.}]
(*  0.398283 + 0. I  *)

OK, so I'm not crazy. : ) I still find it interesting that setting a numeric lower bound but having an exact upper bound (where the discontinuity is) leads to the same issue. I guess MMA treats all the bounds as numeric if one is numeric? — MikeY, Mar 05 '20 at 14:03
@MikeY Yes, the limits all seem to get set to the same precision (the lowest precision, that is, with machine precision being the lowest). — Michael E2, Mar 05 '20 at 16:06

Why do the Integrate and NIntegrate give different results?

1 Answers1

Introduction and summary

Analyzing the problem

Discontinuity

Workarounds