4

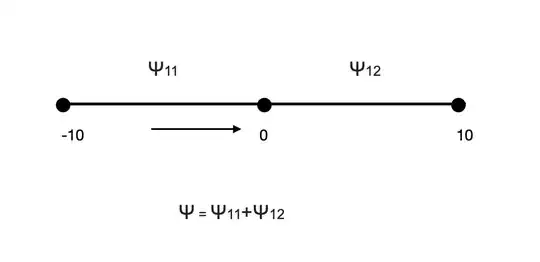
I am trying to create a model of plane wave's propagation on a quantum graph(metric graph with a differential operator, Shrodinger operator in my case, along the edges and continuity condition at the vertices) with given multi-bond transparency boundary conditions at a point 0: My graph's image Shrodinger equation; V = 0 in my case

Given initial and boundary conditions look like this: Conditions

I'm trying to solve it with Mathematica:

initialConditions = {
  u11[0, x] == Sin[Pi*(x + 10)/10]^2,
  u12[0, x] == 0,
  u11[t, -10] == 0,
  u11[t, 0] == 0,
  u12[t, 0] == 0,
  u[t, x] == u11[t, x] + u12[t, x]
  }
boundaryConditions = {
  -I*(3/2)*((D[ u12[t, x], x] /. x -> 0) - (D[u11[t, x], x] /. 
         x -> 0)) + ((D[ u12[t, x], t, x] /. 
        x -> 0) - (D[u11[t, x], t, x] /. x -> 0)) + 
    3*I*((D[ u12[t, x], t] /. x -> 0) - (D[u11[t, x], t] /. 
         x -> 0)) == 0,
  I*D[u11[t, x], t] + (1/2)*D[u11[t, x], {x, 2}] == 0,
  I*D[u12[t, x], t] + (1/2)*D[u12[t, x], {x, 2}] == 0
  }
uix = NDSolveValue[{initialConditions, boundaryConditions}, 
  u, {t, 0, 100}, {x, -10, 0}]

But I keep getting this error: Error

If someone has already experienced such troubles in similar problems, I would highly appreciate any help.

Thanks for your attention.

Update

  1. All functions should be zero at x = ±10.
  2. 11 is defined at [-10, 0], 12 at [0, 10].
  3. I've split one equation for to two for 11 and 12, because otherwise, Mathematica raised an error "system is underdetermined"
  4. I've put {x, -10, 0} because otherwise, I'm getting an error, which states, that 0 is not a boundary, so BC can not be defined. So I decided to split the problem into two calculations(maybe in the wrong way).
user21
  • 39,710
  • 8
  • 110
  • 167
zanhesl
  • 93
  • 6
  • 2
    Hello, welcome to Mathematica.SE. Then, a few questions: 1. What's the b.c. at $x=\pm 10$? 2. Are $\psi_{12}$ and $\psi_{11}$ both defined on $[-10,10]$? 3. In your code you write I*D[u11[t, x], t] + (1/2)*D[u11[t, x], {x, 2}] == 0, I*D[u12[t, x], t] + (1/2)*D[u12[t, x], {x, 2}] == 0, which is inconsistent with the one in the picture, which one is correct? 4. In the code you write {x, -10, 0}, which is again inconsistent with the picture, which one is correct? – xzczd Apr 13 '20 at 10:49
  • Hello, @xzczd, thanks for the answer. 1. All functions should be zero at x = ±10. 2. 11 is defined at [-10, 0], 12 at [0, 10]. 3. I've split one equation for to two for 11 and 12, because otherwise, Mathematica raised an error "system is underdetermined"4. I've put {x, -10, 0} because otherwise, I'm getting an error, which states, that 0 is not a boundary, so BC can not be defined. So I decided to split the problem into two calculations(maybe in the wrong way). – zanhesl Apr 13 '20 at 13:56
  • So you're solving a problem similar to this, in the sense that there's a boundary condition inside the domain? – xzczd Apr 13 '20 at 14:12
  • @xzczd yes, I think in that way it is kind of similar. But the main problem with the "dependent variables in boundary conditions" remains. Maybe you can give me a piece of advice on how to reformulate my boundary condition at 0 to solve it with Mathematica? – zanhesl Apr 13 '20 at 15:03

1 Answers1

5

As mentioned in the comment above, this problem is somewhat similar to this, and harder, because the b.c. at $x=0$ involves first order derivative of $t$, which will lead to bdord warning in this case. (Here is an example about dealing with bdord warning. )

So, again, let's discretize the system in $x$ direction all by ourselves. I'll use pdetoode for the task.

{lb = -10, mb = 0, rb = 10, tmax = 100};

With[{u = u[t, x]}, eq = I D[u, t] + 1/2 D[u, {x, 2}] == 0;
  ic = {u == Sin[Pi (x + 10)/10]^2, u == 0} /. t -> 0;
  {bcl, bcm, bcr} = {u == 0 /. x -> lb, 
                     -3 I/2 D[u, x] + D[u, t, x] + 3 I D[u, t] /. x -> mb, 
                     u == 0 /. x -> rb}];


points = 25; {gridl, gridr} = Array[# &, points, #] & /@ {{lb, mb}, {mb, rb}};
difforder = 2;
(* Definition of pdetoode isn't included in this post,
   please find it in the link above. *)

{ptoofuncl, ptoofuncr} = pdetoode[u[t, x], t, #, difforder] & /@ {gridl, gridr};


del = #[[2 ;; -2]] &;
{odel, oder} = del@#@eq & /@ {ptoofuncl, ptoofuncr};
{odeicl, odeicr} = MapThread[#@#2 &, {{ptoofuncl, ptoofuncr}, ic}];
{odebcl, odebcr} = MapThread[#@#2 &, {{ptoofuncl, ptoofuncr}, {bcl, bcr}}];
odebcm = Equal @@ (#@bcm & /@ {ptoofuncl, ptoofuncr});


odebc = {odebcm, With[{sf = 1}, diffbc[t, sf]@{odebcl, odebcr}]};


sollst = NDSolveValue[{odel, odeicl, oder, Rest@odeicr, odebc}, {u /@ gridl, 
     u /@ gridr}, {t, 0, tmax}, MaxSteps -> Infinity]; // AbsoluteTiming


{soll, solr} = MapThread[rebuild, {sollst, {gridl, gridr}}];


sol = {t, x} [Function] Piecewise[{{soll[t, x], x < mb}}, solr[t, x]];


DensityPlot[sol[t, x] // #, {t, 0, tmax}, {x, lb, rb}, PlotPoints -> 50, 
    Exclusions -> None, ColorFunction -> "AvocadoColors"] & /@ {Re, Im} // GraphicsRow

enter image description here

xzczd
  • 65,995
  • 9
  • 163
  • 468
  • Thank you so much! I'm going to try to apply this approach to a three-bonded star graph by myself. – zanhesl Apr 14 '20 at 09:27