DSolve returns no result

Question

I'd like to solve a partial differential equation on a infinite strip. My code is the following:

eqn = D[u[x, t], {t, 2}] + 2 D[u[x, t], {t, 1}] + u[x, t] == 
   D[u[x, t], {x, 2}];
bc = {Derivative[1, 0][u][0, t] == 0, 
   Derivative[1, 0][u][2 π, t] == 0};
ic = {u[x, 0] == Cos[x], Derivative[0, 1][u][x, 0] == Abs[Cos[x/2]]};
Ω = Rectangle[{0, 2 π}, {0, Infinity}];
DSolve[{eqn, bc, ic}, u[x, t], {x, t} ∈ Ω]

Mathematica returns no result -- what could have possible gone wrong?

Answer 1

DSolve (version 8.0) can't find a solution. Do it numerically.

ndsol = NDSolve[{eqn, bc, ic}, u, {x, 0, 2 Pi}, {t, 0, 10}, 
   MaxStepSize -> {5*10^-3, 10^-2}, AccuracyGoal -> 5, 
   PrecisionGoal -> 5]

Plot3D[Evaluate[u[x, t] /. First@ndsol], {x, 0, 2 Pi}, {t, 0, 10}, 
   PlotRange -> All]

Test

bc[[All, 1]] /. t -> 0 /. First@ndsol

(*   {-5.1341*10^-13, 5.23173*10^-13}   *)

ic[[All, 1]] /. x -> 0 /. First@ndsol

(*   {1., 1.}   *)

Plot3D[Evaluate@Chop[eqn[[1]] - eqn[[2]] /. First@ndsol], 
{x, 0, 2 Pi}, {t, 0, 10}, PlotRange -> 10^-5]

Answer 2

Though DSolve can't handle the problem at the moment, the symbolic solution can be found with the help of finite Fourier cosine transform and its inversion:

eqn = D[u[x, t], {t, 2}] + 2 D[u[x, t], {t, 1}] + u[x, t] == D[u[x, t], {x, 2}];
bc = {Derivative[1, 0][u][0, t] == 0, Derivative[1, 0][u][2 π, t] == 0};
ic = {u[x, 0] == Cos[x], 
   Derivative[0, 1][u][x, 0] == 
    Simplify`PWToUnitStep@PiecewiseExpand[Abs[Cos[x/2]], Reals]};
(* Definition of finiteFourierCosTransform isn't included in this post,
   please find it in the link above. *)
tsetlst = Assuming[{n > 0 && n != 2}, 
      Simplify@finiteFourierCosTransform[{eqn, ic}, {x, 0, 2 Pi}, #]] /. 
     Rule @@@ bc & /@ {0, 2, n} /. HoldPattern@finiteFourierCosTransform[a_, __] :> a
tsollst = u[x, t] /. First@DSolve[#, u[x, t], t] & /@ tsetlst
tsol = Piecewise[{tsollst // Most, {n == 0, n == 2}} // Transpose, tsollst // Last] // 
  FullSimplify
mid = inverseFiniteFourierCosTransform[tsol, n, {x, 0, 2 Pi}]
sol = (mid[[2]] /. {n, C} -> {n, 2, 2} // ReleaseHold) + mid /. {{n, C} -> {n, 3, C}, 
   HoldPattern@Piecewise[, a] :> a}

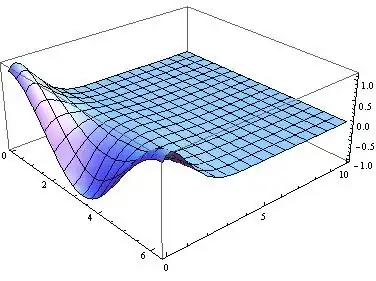
$$u(x,t) = \frac{2 e^{-t} t}{\pi }+\frac{e^{-t} \cos (x) (4 \sin (t)+3 \pi (\sin (t)+\cos (t)))}{3 \pi }+\sum _{n=3}^\infty \frac{\cos \left(\frac{n x}{2}\right) \left(8 \cos \left(\frac{n \pi }{2}\right) \sin \left(\frac{n t}{2}\right) (\sinh (t)-\cosh (t) )\right)}{n \left(n^2-1 \right) \pi}$$

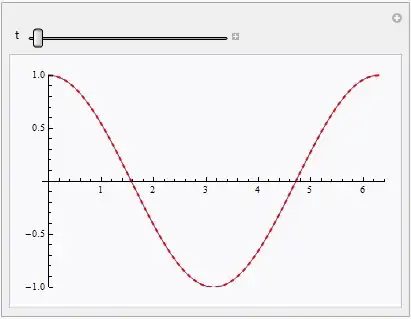
Let's compare it with the numeric solution:

testfunc = Function[{x, t}, #] &[sol /. C -> 30 // ReleaseHold];
mol[n_Integer, o_: "Pseudospectral"] := {"MethodOfLines", 
  "SpatialDiscretization" -> {"TensorProductGrid", "MaxPoints" -> n, 
    "MinPoints" -> n, "DifferenceOrder" -> o}}
nsol = NDSolveValue[{eqn, ic, bc}, u, {t, 0, 4}, {x, 0, 2 Pi}, 
   Method -> mol[50, 4]];
Manipulate[Plot[{testfunc[x, t], nsol[x, t]}, {x, 0, 2 Pi}, PlotRange -> 1, 
  PlotStyle -> {Automatic, {Red, Thick, Dashed}}], {t, 0, 4}]

Remark

1. Abs is transformed to UnitStep so DSolve can solve faster.

2. Finite Fourier cosine transform for $n=0$ and $n=2$ cases have been calculated separately because currently finiteFourierCosTransform, which is built on Integrate, can't handle these two special cases properly when they're hidden behind the symbolic n.

3. sol is just a simplified version of mid.

Answer 3

Infinity does not work with Rectangle. A proper definition can just use Reals instead of Infinity with Elements. Rectangle is not needed, used by Wolfram Inc. for that purpose.

DSolve has on itself an options section for domains.

As shown in the Basic Example for DSolve it is preferable to solve for a pure function u instead of a function u[x,t].

A simple check of the boundary and initial conditions shows, they are inconsistent. The initial condition are inconsistent too. Derivative[0,1] is the derivative to time. It is set to a time-independent function in x with frequency one half.

eqn = D[u[x, t], {t, 2}] + 2 D[u[x, t], {t, 1}] + u[x, t] == 
   D[u[x, t], {x, 2}];
bc = {Derivative[1, 0][u][0, t] == 0, 
   Derivative[1, 0][u][2 π, t] == 0};
ic = {u[x, 0] == Cos[x], Derivative[0, 1][u][x, 0] == Abs[Cos[x/2]]};
ndsol = NDSolve[{eqn, bc, ic}, u, {x, 0, 2 π}, {t, 0, 4.5}]

Mathematica does solve this with the message NDSolve::ibcinc.

Plot3D[Evaluate[u[x, t] /. First@%63], {x, 0, 2 Pi}, {t, 0, 4.5}, 
 PlotRange -> All, AxesLabel -> Automatic]

Boundary conditions are matched well:

bc[[All, 1]] /. t -> 0 /. First@ndsol

(* {-0.000171153, 0.000171153} *)

The boundary values are constant the value for all time.

Initial conditions too:

ic[[All, 1]] /. x -> 0 /. First@ndsol
{1., 1.}

The solution prefers one over the other initial condition on the complete domain.

For example if all bc and is conditions are set to zero, then the message disappears.

Everything is OK with the ic and bc for the solution and it looks:

If it is not possible to get on other paths to the correct bc and ic. Fit them to the general solution of the partial differential equation.