The UnitStep was replaced with the HeavisideTheta after the version 6.0 (reference here), but some differences confused me between the old and the new version as the follows (For convenience, the f[x] is simplified). I want to know how to correct the HeavisideTheta in the Mathematica V11.3 for generating the same results with UnitStep in MM5.2. For the problem, I have proposed some methods( here and here), but which didn't give the result I want. Thanks.
Code in V11.3
f[x_] := 1;
Integrate[f[x]*HeavisideTheta[x], {x, 0, ∞}]
Integrate[f[x]*HeavisideTheta[x], {x, -∞, ∞}]
Integrate[f[x]*D[HeavisideTheta[x], x], {x, 0, ∞}]
Integrate[
f[x]*D[HeavisideTheta[x], x], {x, -∞, ∞}]
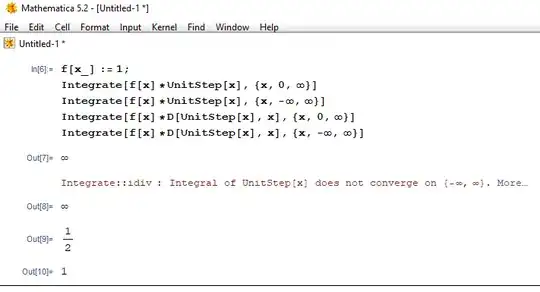
Code in V5.2
f[x_]:=1;
Integrate[f[x]*UnitStep[x],{x,0,∞}]
Integrate[f[x]*UnitStep[x],{x,-∞,∞}]
Integrate[f[x]*D[UnitStep[x],x],{x,0,∞}]
Integrate[f[x]*D[UnitStep[x],x],{x,-∞,∞}]
The results in V11.3
The results in V5.2

HeavisideTheta[0] == 1/2, but you mentioned you wantHeavisideTheta[0]to be1here. Does your goal change? Or this is a special case? – xzczd May 11 '20 at 04:05UnitStepin v5.2 is inconsistent,f[Infinity] UnitStep[Infinity] - f[0] UnitStep[0] - Integrate[f'[x] UnitStep[x], {x, 0, Infinity}]gives0. – xzczd May 11 '20 at 07:13HeavisideTheta[0]to be 1, becauseUnitStep[0]=1in V5.2 (you can check it through the help document of V5.2), I just want to realize the function ofUnitStepin V5.2 by using theHeavisideThetainV11.3 (HeavisideTheta, no value in 0 point). But today, this time, the 3rd example show us thatHeavisideTheta[0]should be 1/2, they will give the same result. In a word, on the one hand,HeavisideTheta[0]should be 1 becauseUnitStep[0]=1in V5.2, on the other hand,HeavisideTheta[0]should be 1/2 because the 3rd example. – likehust May 11 '20 at 12:07UnitStepin v5.2 is self-contradictory. If your legacy code has made use of such feature, then things become a little troublesome. It's not too hard to find work-around for this 4 examples, but I doubt if the solution can be extended to more general cases. Do you have something, say, a complete summarization of the feature ofUnitStepin v5.2? Or perhaps you can show a bigger example indicating what exactly you're trying to do? – xzczd May 12 '20 at 01:28Integrate::idivwarning and return unevaluated so I can't check further, but I wonder what's the output ofIntegrate[-UnitStep[x],{x,0,∞}]andIntegrate[-UnitStep[x],{x,-∞,∞}]in v5.2? – xzczd May 13 '20 at 02:01Integrate[-UnitStep[x],{x,0,∞}]gives-∞, andIntegrate[-UnitStep[x],{x,-∞,∞}]givesIntegrate::idiv: Integral of UnitStep[x] does not converge on {-∞,∞}, -∞. Hope it helps you find the answer. – likehust May 13 '20 at 03:17