Tangent to a circle

Question

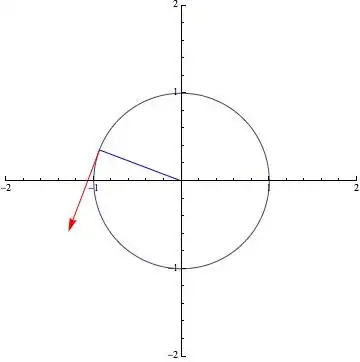
I am trying to show vector of fixed length which is the tangent to a circle which rotates. Any suggestions on how to simplify this ? My question is not about using Manipulate etc but more is there an easier way to compute and draw the tangent ?

x[t_] := Cos[t];
y[t_] := Sin[t];
d[x_, y_] := If[y == 0, 0, -x/y];
tangent[1, 0] = Arrow[{{1, 0}, {1, 1}}];
tangent[-1, 0] = Arrow[{{-1, 0}, {-1, -1}}];
tangent[0, -1] = Arrow[{{0, -1}, {1, -1}}];
tangent[0, 1] = Arrow[{{0, 1}, {1, 1}}];
tangent[x_, y_] = 
  If[y > 0, 
   Arrow[{{x, y}, {x - Cos[ArcTan[d[x, y]]], 
      y - Sin[ArcTan[ d[x, y]]]}}],
   Arrow[{{x, y}, {x + Cos[ArcTan[d[x, y]]], 
      y + Sin[ArcTan[ d[x, y]]]}}]];
Manipulate[
 p = ParametricPlot[{x[t], y[t]}, {t, 0, 2 π}, 
   PlotRange -> {-2, 2}];
 g = Graphics[{{Blue, Line[{{0, 0}, {x[a], y[a]}}]}, {Red, 
     tangent[x[a], y[a]]}}];
 Show[{p, g}],
 {a, 0, 2 π}]

Moving tangent

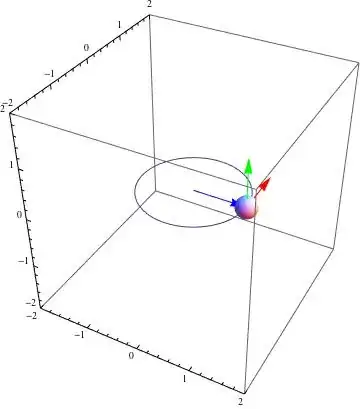
I extended my example above to include a 3D solution using suggested solutions -

Module[{x,y,z,tangent},
x[t_]:=Cos[t];
y[t_]:=Sin[t];
z[t_]:=0;
r ={{-2,2},{-2,2},{-2,2}};
p=ParametricPlot3D[{x[t],y[t],z[t]},{t,0,2π},PlotRange->r,BoxRatios->1];
tangent[x_,y_,z_]:={Red,Arrow[{{x,y,z},{x-y,x+y,z}}]};
Manipulate[
g :=Graphics3D[{Sphere[{x[t],y[t],z[t]},0.2],
{Green,Arrow[{{x[t],y[t],z[t]},{x[t],y[t],1}}]},
{Blue,Arrow[{{0,0,0},{x[t],y[t],z[t]}}]},
tangent[x[t],y[t],0]
},PlotRange->r,BoxRatios->1];
Show[p,g],
{t,0,4π}
]
]

This question, as a special case of finding unit tangent ... vectors, finds many (excellent) answers there. — whuber, Mar 27 '13 at 18:11

score 3 · Answer 1 · edited Jun 08 '17 at 16:05

3

If all you need is a tangent to a circle, and not a tangent to an arbitrary curve, you can just rotate an arrow:

Manipulate[
 Graphics[{Circle[], Rotate[Arrow[{{1, 0}, {1, 1}}], φ, {0, 0}]}],
 {φ, 0, 2 Pi}
]

You may also be interested in the two-argument form of ArcTan[x,y] (look it up in the docs).

edited Jun 08 '17 at 16:05

LCarvalho

9,233
4
40
96

answered Mar 27 '13 at 17:18

Szabolcs

234,956
30
623
1,263

Thank you. Will checkout both suggestions. – David McHarg Mar 27 '13 at 17:26

score 2 · Answer 2 · edited Jun 08 '17 at 16:07

2

Without Rotate:

ctangent[x_, y_] := Arrow[{{x, y}, {x - y, x + y}}]
Manipulate[
 Graphics[{Circle[], {Blue, Line[{{0, 0}, {x[a], y[a]}}]}, {Red, 
    ctangent[x[a], y[a]]}}, 
    PlotRange -> {{-2, 2}, {-2, 2}}, 
    Axes -> True], {a, 0, 2 π} 
]

edited Jun 08 '17 at 16:07

LCarvalho

9,233
4
40
96

answered Mar 27 '13 at 17:32

halmir

15,082
37
53

Thanks. Never thought of that. Excellent. As i can use this solution in 3D as well. – David McHarg Mar 27 '13 at 17:43

Dr. belisarius · Answer 3 · 2013-03-27T18:06:22.360

1

a = {{0, 0}, {1, 0}, {1, 1}}; 
Manipulate[
 Graphics[{Circle[], 
           Rotate[{Line@a[[;;2]], Arrow[a[[2;;]]]}, x, {0, 0}]}, 
           PlotRange -> {{-2, 2}, {-2, 2}}, Axes -> True], 
{x, 0, 2 Pi}]

edited Mar 27 '13 at 18:06

answered Mar 27 '13 at 17:24

Dr. belisarius

115,881
13
203
453

Tangent to a circle

3 Answers3

Linked