3

My code is

Integrate[ 1/Sqrt[(x - a) (x - b) (x - c) (x - d)], {x, a,  ∞}, 
           Assumptions -> 0 < d < c < b < a]

I know this can be expressed be the incomplete elliptic integral of first kind (EllipticF), but the output remains unevaluated

Integrate[ 1/Sqrt[(-a + x) (-b + x) (-c + x) (-d + x)], {x, a,  ∞}, 
           Assumptions -> 0 < d < c < b < a]

Why does this happen? I am desperate

Artes
  • 57,212
  • 12
  • 157
  • 245
Filippo Caleca
  • 133
  • 6
  • 1
    If the output is echoed, it means Mathematica doesn't know what to do with it. – J. M.'s missing motivation May 20 '20 at 12:02
  • Seems to work OK for the indefinite integral. And the result can be evaluated at a and Infinity using the Limit function – Gustavo Delfino May 20 '20 at 12:09
  • But isn't it strange Mathematica can't calculate it? I also tried changing the integration from a to a generic M but the result is the same. From Gradshteyn Ryzhik I know this is equal to EllipticF(...,...), should I doubt the tables of Gradshteyn Ryzhik or is it common that Mathematica can't do integrals like this one? – Filippo Caleca May 20 '20 at 12:11

2 Answers2

8

Actually V 12.1 can do it directly, you just have to wait a little bit long:

Clear["Global`*"];

int = Integrate[1/Sqrt[(x - a) (x - b) (x - c) (x - d)], {x, a, Infinity}, 
               Assumptions -> 0 < d < c < b < a]

enter image description here

May be OP used different Mathematica version? It will be good to post which version was used. Screen shot below:

enter image description here

Old answer

A Workaround for now: (assuming proper integral)

 int = Integrate[1/Sqrt[(x - a) (x - b) (x - c) (x - d)], x]

enter image description here

low = Assuming[0 < d < c < b < a, Limit[int, x -> a]]
(* 0 *)

high = Assuming[0 < d < c < b < a, Limit[int, x -> Infinity]]

enter image description here

The above is then the final result.

Nasser
  • 143,286
  • 11
  • 154
  • 359
  • 1
    Thank you! I am using 11.3 – Filippo Caleca May 20 '20 at 12:52
  • 2
    @FilippoCaleca integrate in V12.1 has improved over 11.3 – Nasser May 20 '20 at 12:56
  • my output is different, in fact writing: int = Integrate[1/Sqrt[(x - a) (x - b) (x - c) (x - d)], x]
    the output is -((2 (-a + x) (-b + x) Sqrt[((a - b) (-c + x))/((b - c) (a - x))] Sqrt[((a - b) (-d + x))/((b - d) (a - x))] EllipticF[ ArcSin[Sqrt[((a - d) (-b + x))/((b - d) (-a + x))]], ((a - c) (b - d))/((b - c) (a - d))])/((a - b) Sqrt[((a - d) (b - x))/((b - d) (a - x))] Sqrt[(-a + x) (-b + x) (-c + x) (-d + x)]))

    the argument of EllipticF are different, how is it?

     – Filippo Caleca May 20 '20 at 13:09
  • @FilippoCaleca I do not know why 11.3 gives a little bit different antiderivative than V 12.1. It is possible there was an improvement made, or even a fix. I do not know. It is always to use latest release as each release improves over the last one. – Nasser May 20 '20 at 13:17
  • 2
    Note that you shouldn't expect the technique used in your workaround to work in all cases. See this old Wolfram blog post for some of the mathematical nitty-gritty as to why. – Michael Seifert May 20 '20 at 19:58
  • @MichaelSeifert Yes I know. But I said assuming proper integral. Isn't this enough condition to allow one to use F.T.C. like I did above on it? – Nasser May 20 '20 at 20:45
  • Not always — that's the point of the blog post. Compare the results of f[x_] = Integrate[1/(2 + Sin[x]), x]; f[2 Pi] - f[0] and Integrate[1/(2 + Sin[x]), {x, 0, 2 Pi}]. Then plot 1/(2+Sin[x]) from 0 to 2π and see which result you think is correct. – Michael Seifert May 20 '20 at 21:06
  • @MichaelSeifert that is the fault of Mathematica's antiderivative actually. If you use Rubi, you'll get same result in both cases. Here is screen shot Mathematica graphics – Nasser May 20 '20 at 21:15
  • As Michael mentions, one has to be careful; see e.g. this. – J. M.'s missing motivation May 21 '20 at 00:39
  • @J.M.'stechnicaldifficulties I know one has to be careful. That is why I said, assuming proper integral. Would you have an example of a proper integral where one can not apply the F.T.O.C. on it? I am using this definition of proper integral At school I learned if integral is proper, then anti-derivative should not have discontinuities as well. i.e. continuities integrand, defined everywhere in its integration range (i.e. proper) should have continuities antiderivative (optimally so). Rubi here gives optimal one. Mathematica did not. – Nasser May 21 '20 at 00:56
  • Even though both Rubi's result And Mathematica's for Integrate[1/(2 + Sin[x]),x] are correct in the sense that differentiating the anti-derivative gives back the integrand, Mathematica`s result is discontinuous while Rubi's is not. In both cases the integral here is proper. This is why FTOC failed here when using Mathematica's result. But this is only because Mathematica's anti-derivative is not optimal. – Nasser May 21 '20 at 01:01
  • The blog post linked by @Michael does have that example you have in mind: $$\int_0^{2\pi}\frac{\mathrm dx}{5+4\sin x}$$ – J. M.'s missing motivation May 21 '20 at 01:01
  • "this is only Mathematica's anti-derivative is not optimal." - I could agree with that. But it is also difficult in general to generate an antiderivative that is guaranteed to be continuous over a desired interval of integration. – J. M.'s missing motivation May 21 '20 at 01:02
  • @J.M.'stechnicaldifficulties Are you sure this integral is proper? According to FriCAS, it found a pole between $0\dots 2\pi$. Please see ii:=integrate(1/(5+4*sin(x)),x=0..2*%pi) "potentialPole" but will look into it. Thanks also for the example. – Nasser May 21 '20 at 01:22
  • If you plot $1/(5+4\sin x)$ over its integration interval, you won't see a pole. But the discontinuity of the "easy" antiderivative at $x=\pi$ is precisely the source of the problem, as noted in that blog entry. – J. M.'s missing motivation May 21 '20 at 01:26
  • @J.M.'stechnicaldifficulties So the main question I pose is this: If the integrand is continuities everywhere over the integration range (i.e proper integral), should the "optimal" anti-derivative always be continuities as well? Not what Mathematica or any other program gives as antiderivative, but mathematically speaking. My understand was it should, but such optimal anti-derivative could be hard to find, yes. – Nasser May 21 '20 at 01:36
  • 2
    Sure, if you go back to the concept of "area under a curve", then one might expect that an antiderivative ought to be continuous if the original function is continuous. But yes, it's not always easy to do. That's why Mathematica has to try harder for definite integrals, tho it has been known to still make mistakes sometimes. – J. M.'s missing motivation May 21 '20 at 01:41
  • Moreover, if you want to find an "anti-derivative" that works for all complex values of a function (i.e., given $f(z)$, find a complex function $F(z)$ for which $dF/dz = f(z)$), it is in general impossible to find a continuous $F(z)$. Any simple poles in $f(z)$ will lead to branch cuts in $F(z)$. You still have some freedom in where to direct these branch cut (and maybe you can keep them away from the real axis if you're clever), but you won't be able to find an antiderivative that is continuous everywhere in the complex plane. – Michael Seifert May 21 '20 at 13:39
6

In the newest version (i.e. 12.1) this integral evaluates a bit long, however changing the variable $x \mapsto t = x-a\;$ this can be evaluated a few times faster. 

int2 = Integrate[ 1/Sqrt[t (t + a - b) (t + a - c) (t + a - d)], {t, 0, ∞}, 
                  Assumptions -> 0 < d < c < b < a]

2 EllipticF[ ArcSin[ Sqrt[(b - d)/(a - d)]], 
               ((b - c)(a - d))/((a - c)(b - d))]/Sqrt[(a - c)(b - d)]

TraditionalForm[%]

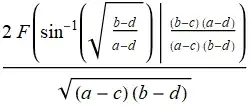
enter image description here

I'm working with the system in cloud and sometimes it appears that the integral in question may remain unevaluated while int2 evaluates well even in version 11.2 on my machine.

Mathematica functions evolve with time even if its usage remains tha same. This aspect of the system is perhaps the most obvious in case of symbolic integration (Integrate), exact solutions of differential equations (DSolve) and the special functions (among them EllipticF). Elliptic functions and integrals appeared in Mathematica 1, however since then many new related functionalities would have been added later e.g. EllipticF was introduced in version 1.0 year 1988 and updated in 3.0 (1996). WeierstrassP was introduced in version 1.0 and updated in 3.0 (1996), however several new functionalities related appeared in version 11.2 (2017) like e.g. WeierstrassHalfPeriodW1 or WeierstrassE1 see e.g. this answer Integrate yields complex value, while after variable transformation the result is real. Bug?. Inspecting another answers therein one can see how Integrate can be sensitive when new functions or functionalities appear. It relates not only to new functionalities but also to widening domain of existing functions (in documentation pages one finds information when a function was introduced and when it was last updated, nevertheless there are also hiden changes that are not reported, however they may be crucial when certain different functions involved were updated). One should take attention to this aspect related to better handling of symbolic input of e.g. WeierstrssHalfPeriodW1 in version 12.1 with respect to 11.2 and it is advantageous to pay atention to this post. Elliptic functions and integrals play very important role in mathematics, physics, engineering and they are still better handled in newer versions of the system. This does not mean that Mathematica is defective but rather that perfect handling of special functions can be approached asymptotically and it is still in interest of developers of the system, e.g. one of leading experts in the field of special functions Oleg Marichev is a member of the special functions group in WRI. Having said that we can accept the state of art and the fact that things can change at least on the symbolic level.

Let's come back to version 11.2 with help of a simple change of variables: $$ x \mapsto t+a$$

int3 = Integrate[ 1/Sqrt[t (t + a - b) (t + a - c) (t + a - d)], {t, 0, ∞}, 
                  Assumptions -> 0 < d < c < b < a]

(2 (EllipticF[ ArcSin[Sqrt[(a - d)/(b - d)]], ((a - c) (b - d))/((b - c) (a - d))]
  + I EllipticK[((a - b) (c - d))/((-b + c) (a - d))]))/Sqrt[(b - c) (a - d)]

TraditionalForm[%]

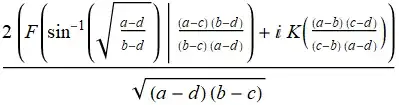
enter image description here

This might seem strange that there appears an imaginary number however the full integral is indeed real even though FullSimplify cannot demonstrate (in 11.2) that both results are equal. In 12.1 this still cannot be done, although a simpler identity can be proved, assuming that parameters are related somehow (in 12.1 not in 11.2), e.g.

FullSimplify[(8(EllipticF[ArcSin[Sqrt[3/2]], 4/3] + 
              I EllipticK[-(1/3)]))/(Sqrt[3] Sqrt[a^2]) 
              - (4 EllipticF[ArcSin[Sqrt[2/3]], 3/4])/Sqrt[a^2], a > 0]

0

We can show that this is the case evaluating numerically, e.g.

With[{a = 4, b = 3, c = 2, d = 1}, {
 (2 (EllipticF[ ArcSin[Sqrt[(a - d)/(b - d)]], ((a - c) (b - d))/((b - c) (a - d))] 
+ I EllipticK[((a - b) (c - d))/((-b + c) (a - d))]))/Sqrt[(b - c) (a - d)], 
( 2 (EllipticF[ ArcSin[Sqrt[(b - d)/(a - d)]], 
               ((b - c)(a - d))/((a - c)(b - d))]))/Sqrt[(a - c)(b - d)]} // N // Chop]

{1.07826, 1.07826}

For example of a bit more testy case see e.g. Why does Integrate declare a convergent integral divergent?

Making appropriate plot of the functions and their difference might be helpful as well:

Plot[{#, # - (4 EllipticF[ArcSin[Sqrt[2/3]], 3/4])/Sqrt[a^2]}, {a, 0, 6},
  PlotStyle -> Thick, AxesOrigin -> {0, 0}] &[ (
8(EllipticF[ArcSin[Sqrt[3/2]], 4/3] + I EllipticK[-1/3]))/(Sqrt[3]Sqrt[a^2])]

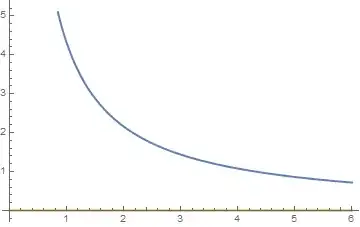
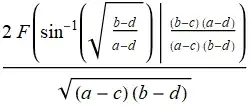
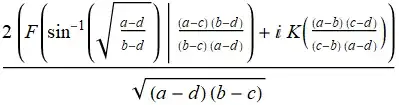
enter image description here

Artes
  • 57,212
  • 12
  • 157
  • 245