You can mash up some of the answers from the football question
$3D$ graphic of soccer ball
Credit to J. M.'s technical difficulties♦ and MarcoB as this draws on those answers:
arc[center_?VectorQ, {start_?VectorQ, end_?VectorQ}] :=
Module[{ang, co, r}, ang = VectorAngle[start - center, end - center];
co = Cos[ang/2]; r = EuclideanDistance[center, start];
BSplineCurve[{start,
center + r/co Normalize[(start + end)/2 - center], end},
SplineDegree -> 2, SplineKnots -> {0, 0, 0, 1, 1, 1},
SplineWeights -> {1, co, 1}]]
curvedEdges[polyh_] :=
ReplaceAll[MeshPrimitives[polyh, 1],
Line[coords_] :> arc[{0, 0, 0}, coords]];
draw[poly_] :=
Block[{r = Norm[MeshPrimitives[poly, 0][[1, 1]]]},
Graphics3D[{EdgeForm[],
MeshPrimitives[poly, 2] /.
p : Polygon[l_] :> {If[Length[l] > 3, Orange, Yellow],
GraphicsComplex[r (Normalize /@ MeshCoordinates[#]),
MeshCells[#, 2]] &@
DiscretizeRegion[p, MaxCellMeasure -> {"Area" -> 0.0025}]},
curvedEdges[poly]
}, Boxed -> False, Lighting -> "Neutral"]]
draw[TruncatedPolyhedron[Dodecahedron[]]]
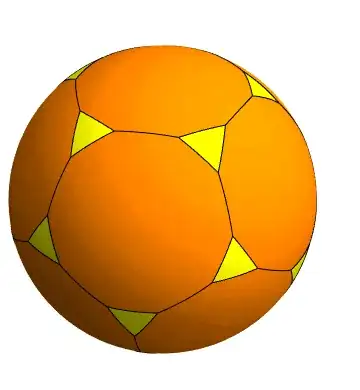


TruncatedPolyhedron[Dodecahedron[], 0.3]. In v11 you'll need to use thePolyhedronOperationspackage:<< PolyhedronOperations`; Truncate[PolyhedronData["Dodecahedron"], .3]– flinty Jun 12 '20 at 17:21