1

I have two functions f[x,y] and g[x,y] calculated on a grid {x,y}. Then I perform numerical Fourier transforms,

FTf=Fourier[dataf]; 
FTg=Fourier[datag]

I am looking for convolution $w=f*g$. To calculate it, I do

listw=InverseFourier[FTf*FTg]

and finally I would like to plot density of $w$. To do it, I reshape listw and then construct list data={{x1,y1,w1},...} and finally

ListDensityPlot[data]

Everything seems ok but the final plot is quite strange. Is everything ok with my derivation?

To be specific, the following code presents the simpler version:

f[x_, y_] := Exp[-(x^2 + y^2)];
g[x_, y_] := Exp[-4*(x^2 + y^2)];
fdata = Table[f[x, y], {x, -1, 1, 0.1}, {y, -1, 1, 0.1}];
gdata = Table[g[x, y], {x, -1, 1, 0.1}, {y, -1, 1, 0.1}];
FTf = Fourier[fdata];
FTg = Fourier[gdata];
listw = InverseFourier[FTf*FTg];
wvalues = Abs[ArrayReshape[listw, 21^2]];
xypairs = Flatten[Table[{x, y}, {x, -1, 1, 0.1}, {y, -1, 1, 0.1}], 1];
data = ArrayReshape[Transpose[{xypairs, wvalues}], {21^2, 3}];
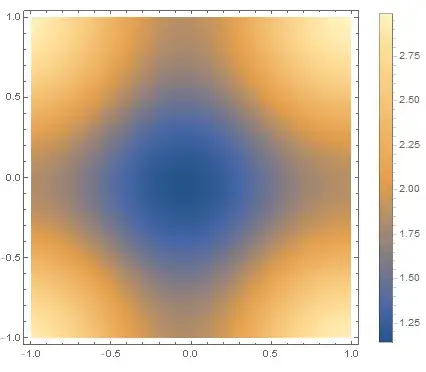
ListDensityPlot[data]

which produces plot:

enter image description here

For simple functions, I can calculate FT explicitly:

FTf1 = FourierTransform[f[x, y], {x, y}, {w1, w2}];
FTf2 = FourierTransform[g[x, y], {x, y}, {w1, w2}];
wfunction = InverseFourierTransform[FTf1*FTf2, {w1, w2}, {x, y}]

and then can density plot wfunction[x_,y_]:

enter image description here

Artem Alexandrov
  • 803
  • 4
  • 11
  • Can you share the data as well? Also, why is the plot "strange"? That is, what had you expected and how is the output different from that? – MarcoB Jun 18 '20 at 18:19
  • @MarcoB the data is huge arrays, I try to realize the simpler example. – Artem Alexandrov Jun 18 '20 at 18:20
  • @MarcoB I have tried to provide the simple example of my code. I assume that the problem comes from manipulations with xy-grid and array reshaping. – Artem Alexandrov Jun 18 '20 at 18:42

2 Answers2

3

Let's compare convolution in the time domain and the spatial domain. Consider the convolution of two signals h and x.

h = {1, -1, 2, -2, 3, -3};  
x = {1, 2, 3, 4, 5, 6, -5, -4, -3, -2, -1};  
n = Length[x] + Length[h] - 1;
xPad = PadRight[x, n];

The convolution is:

yConv = ListConvolve[h, xPad, {1, 1}]

{1, 1, 3, 3, 6, 6, -6, 6, -18, 6, -30, 6, 5, 5, 3, 3}

Using the FFTs of h and x:

ffth = Fourier[PadRight[h, n], FourierParameters -> {1, -1}];
fftx =  Fourier[PadRight[x, n], FourierParameters -> {1, -1}];
yFourier = InverseFourier[ffth fftx, FourierParameters -> {1, -1}]

(same as above)

The padding is used in the Fourier because both signals must have the same length. The padding in the time domain is needed because you want to implement circular convolution in order to be the same as the Fourier method.

bill s
  • 68,936
  • 4
  • 101
  • 191
  • To be honest, I do understand Yours answer clearly. In my example both arrays fdata and gdata have the same length. Could you please clarify your answer? – Artem Alexandrov Jun 18 '20 at 20:01
  • If your two data sequences already have the same length then you can ignore/remove the padding. – bill s Jun 18 '20 at 22:46
1

This happens because Fourier puts the zero frequency Fourier component at the beginning of the output list.

center[array_] := 
RotateRight[Map[RotateRight[#, Floor[Length[array]/2]] &, array], 
Floor[Length[array]/2]]

f[x_, y_] := Exp[-(x^2 + y^2)];
g[x_, y_] := Exp[-4*(x^2 + y^2)];
fdata = Table[f[x, y], {x, -1, 1, 0.1}, {y, -1, 1, 0.1}];
gdata = Table[g[x, y], {x, -1, 1, 0.1}, {y, -1, 1, 0.1}];
FTf = center[Fourier[fdata]];
FTg = center[Fourier[gdata]];
listw = center[InverseFourier[FTf*FTg]];
wvalues = Abs[ArrayReshape[listw, 21^2]];
xypairs = Flatten[Table[{x, y}, {x, -1, 1, 0.1}, {y, -1, 1, 0.1}], 1];
data = ArrayReshape[Transpose[{xypairs, wvalues}], {21^2, 3}];
ListDensityPlot[data]

enter image description here

ulvi
  • 1,808
  • 10
  • 15
  • I would like to ask one more question: it seems that numerical Fourier is quite inaccurate (cf. numerical and explicit plots)... What can I do to fix it? – Artem Alexandrov Jun 19 '20 at 13:27
  • Discrete sampling is equivalent to bandwidth limiting your Fourier transform (see Nyquist's sampling theorem etc); in other words when you discretely sample your functions you are in effect truncating your Fourier transforms above a certain cutoff frequency, and that's causing the reconstruction via the inverse Fourier to be inaccurate. – ulvi Jun 20 '20 at 07:28