Multi-peak fitting and area of the fitting

Question

I am trying to fit 3 peaks to the following data:

https://pastebin.com/QCAKwZ2P

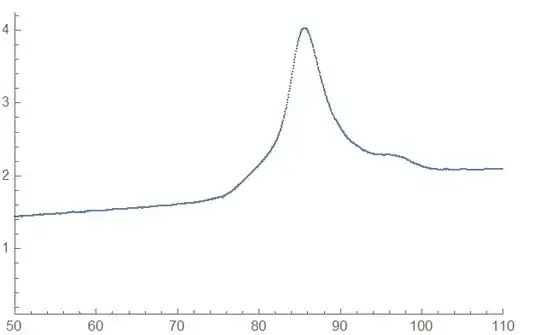
which plotted using ListPlot[data, PlotRange -> {{50, 110}, {0.1, All}}] gives:

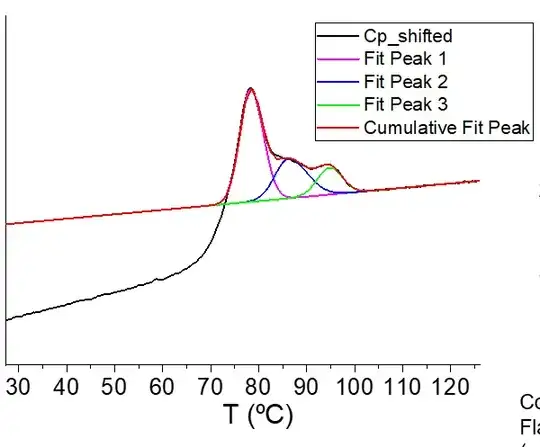
I want to fit three peaks similar to the figure below (done with Origin software), which has a baseline based on on the data line from about 104 to above.

I tried incorporating what I found in this amazing post: How to perform a multi-peak fitting? , but I was unsuccessful to do it automatically for my problem.

Question:

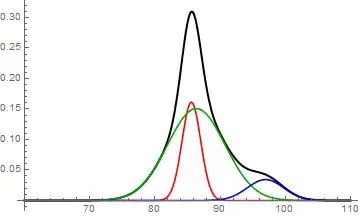
1. How can I fit three peaks for this data automatically (I think using three gaussian peaks should give an acceptable result as I show below)?
2. How can I find the areas of those fits?

Thank you very much

EDIT ON WHAT I HAVE DONE:

This is one code I was able to do using Manipulate

baseline = LinearModelFit[Select[data, 104 <= #[[1]] <= 150 &], x, x];
map = MapAt[baseline, data[[1 ;; All, 1]], { ;; }];
curvLoc=data - map; (*This makes the plot to be centered at zero*)
background = ListPlot[curvLoc, PlotRange -> All, ImageSize -> Large]

Here I used three normal distribution fits:

model = height + amp1*Exp[-(x - x01)^2/sigma1^2] + 
  amp2*Exp[-(x - x02)^2/sigma2^2] + amp3*Exp[-(x - x03)^2/sigma3^2]
findBestFitFromValues[{amp1guess_, x01guess_, sigma1guess_, 
   amp2guess_, x02guess_, sigma2guess_, amp3guess_, x03guess_, 
   sigma3guess_, heightguess_}] :=
 FindFit[curvLoc, {model, {sigma1 > 0, sigma2 > 0, 
    sigma3 > 0}}, {{amp1, amp1guess}, {x01, x01guess}, {sigma1, 
    sigma1guess}, {amp2, amp2guess}, {x02, x02guess}, {sigma2, 
    sigma2guess}, {amp3, amp3guess}, {x03, x03guess}, {sigma3, 
    sigma3guess}, {height, heightguess}}, 
  x](*This is a function that takes guesses and finds the best fit. \
Sigma was constrained to be positive.*)

Using Manipulate:

 With[
 {
  localModel =
   model /.
    {
     amp1 -> amp1Var, amp2 -> amp2Var, amp3 -> amp3Var,
     sigma1 -> sigma1Var, sigma2 -> sigma2Var, sigma3 -> sigma3Var,
     x01 -> x01Var, x02 -> x02Var, x03 -> x03Var,
     height -> heightVar
     }},
 Manipulate[
  Column[{
    Style["Match to Data", 12, Bold],
    Show[background, Plot[localModel, {x, 0, 150}, PlotRange -> All], 
     Graphics[
      {
       Orange, Line[{{x01Var, 0}, {x01Var, 150}}],
       Blue, Line[{{x02Var, 0}, {x02Var, 150}}],
       Red, Line[{{x03Var, 0}, {x03Var, 150}}]
       }
      ]],
    Style["Final Curve", 12, Bold],
    Plot[localModel, {x, 60, 120}, PlotRange -> Full]}
   ],
  Delimiter, Style["Peak 1", 12, Bold],
  {{amp1Var, 1.97, Style["Amplitude 1", Orange]}, 0, 4},
  {{x01Var, 83.6, Style["Center 1", Orange]}, 0, 120},
  {{sigma1Var, 2.93, Style["sigma 1", Orange]}, 0, 5},
  Delimiter, Style["Peak 2", 12, Bold],
  {{amp2Var, 0.342, Style["Amplitude 2", Blue]}, 0, 1},
  {{x02Var, 90, Style["Center 2", Blue]}, 0, 120},
  {{sigma2Var, 1.51, Style["sigma 2", Blue]}, 0, 5},
  Delimiter, Style["Peak 3", 12, Bold],
  {{amp3Var, 0.218, Style["Amplitude 3", Red]}, 0, 1},
  {{x03Var, 94.8, Style["Center 3", Red]}, 0, 120},
  {{sigma3Var, 2.92, Style["sigma 3", Red]}, 0, 5},
  Delimiter, Style["Height", 12, Bold],
  {{heightVar, 0, Style["Height"]}, -0.5, 2},
  Delimiter, Style["Obtained Values", 12, Bold],
  Row[{
    Dynamic[
     {
      Set[amp1UserDefined, amp1Var],
      Set[x01UserDefined, x01Var],
      Set[sigma1UserDefined, sigma1Var],
      Set[amp2UserDefined, amp2Var],
      Set[x02UserDefined, x02Var],
      Set[sigma2UserDefined, sigma2Var],
      Set[amp3UserDefined, amp3Var],
      Set[x03UserDefined, x03Var],
      Set[sigma3UserDefined, sigma3Var],
      Set[heightUserDefined, heightVar]}, "  "
     ]}],
  SaveDefinitions -> True
  ]
 ]

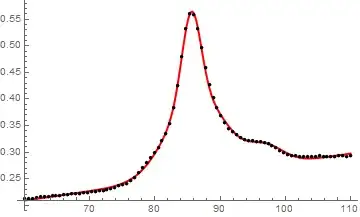
I get:

I found the areas as this:

curve1 = Integrate[
  amp1UserDefined*
   Exp[-(x - x01UserDefined)^2/sigma1UserDefined^2], {x, 70, 120}]
curve2 = Integrate[
  amp2UserDefined*
   Exp[-(x - x02UserDefined)^2/sigma2UserDefined^2], {x, 70, 120}]
curve3 = Integrate[
  amp3UserDefined*
   Exp[-(x - x03UserDefined)^2/sigma3UserDefined^2], {x, 70, 120}]

This code works well but the problem I have is that I would like the fits to be found automatically and not to require the input of the user (hence I would like it without Manipulate)

Answer 1

Isolate the area of interest with the peaks:

peak = Select[data, 60 <= First[#] <= 110 &];
ListPlot[peak]

Helper function to define a Gaussian-shaped peak:

ClearAll[gaussmodel]
gaussmodel[height_, width_, position_] := height Exp[-(x - position)^2/(2 width^2)]

Carry out the fitting, with some appropriate initial values, as well as a sloping baseline added in:

nlm = NonlinearModelFit[
   peak,
   Sum[gaussmodel[height[i], width[i], position[i]], {i, 3}] + slope x + baseline,
   {slope, baseline, 
    height[1], width[1], {position[1], 86}, 
    height[2], width[2], {position[2], 93}, 
    height[3], width[3], {position[3], 97}},
   x
];
nlm["BestFitParameters"]
(* Out: 
{slope -> 0.00176747, baseline -> 0.103191, 
 height[1] -> 0.161099, width[1] -> 1.43419, position[1] -> 85.6025, 
 height[2] -> 0.150749, width[2] -> 4.40078, position[2] -> 86.3575, 
 height[3] -> 0.0343556, width[3] -> 2.78999, position[3] -> 96.9584} *)

Note that there are A LOT of parameters here; for instance, the decision to fit three peaks is not really supported by the data, but I just went with what you wanted. Many of these parameters are also highly correlated:

(nlm["CorrelationMatrix"] /. v_ :> Style[v, Red] /; 0.7 <= Abs[v] < 1) // MatrixForm

The fit is (unsurprisingly) visually pretty good:

Show[
  Plot[
    nlm[x], Evaluate@Flatten@{x, MinMax@peak[[All, 1]]},
    PlotStyle -> Directive[Thick, Red]
  ],
  ListPlot[peak[[;; ;; 10]], PlotStyle -> Black]
]

Below are the single components of the fit. They are different from the ones you found in Origin, which is unsurprising because I expect the results of this fit to be HIGHLY DEPENDENT on the initial conditions. If you don't like these results, use more appropriate initial conditions in the NonlinearModelFit.

Show[
 (* fitted peak - baseline *)
 Plot[
   nlm[x] - (slope x + baseline) /. nlm["BestFitParameters"],
   Evaluate@Flatten@{x, MinMax@peak[[All, 1]]},
   PlotStyle -> Directive[Thick, Black]
 ],
 (* single components *)
 MapThread[
  Plot[#1, Evaluate@Flatten@{x, MinMax@peak[[All, 1]]}, PlotStyle -> #2, PlotRange -> All] &,
  {
   Table[gaussmodel[height[i], width[i], position[i]] /. nlm["BestFitParameters"], {i, 3}],
   {Red, Darker@Green, Blue}
  }
 ]
]

And finally, the areas of those peaks, corresponding to the peaks in red, green, and blue above, respectively:

NIntegrate[
  Table[gaussmodel[height[i], width[i], position[i]] /. nlm["BestFitParameters"], {i, 3}],
  Flatten@{x, MinMax@peak[[All, 1]]}
]
(* Out: {0.579148, 1.66293, 0.240264} *)

For convenience you can also get a relative area (as a percentage) using e.g. 100 Normalize[%, Total].