Finding the maximum of a piecewise function

Question

I have the following piecewise function of the variable $e_f$:

$$g(a,b,c,w,F,e_h,e_f)=\begin{cases} \frac{(c-a e_f) (e_f (4e_f w-a)+c)}{8 b e_f^2} & \left(e_f=e_h\land e_f>\frac{c}{a}\right)\lor e_f\geq \frac{c}{a-2 \sqrt{b} \sqrt{F}} \\ 0 & \text{otherwise} \end{cases} $$

where all the parameters $a$, $b$, $c$, $w$, $F$, $e_h$ and $e_f$ are strictly positive ($\gt 0$).

g[a_, b_, c_, w_, F_, eh_, ef_] := Piecewise[{{
    ((c - a ef) (c + ef (-a + 4 ef w)))/(8 b ef^2),
      (ef == eh && ef > c/a) || ef >= c/(a - 2 Sqrt[b] Sqrt[F])
  }}, 0]

For given numerical values of $a$, $b$, $c$, $w$, $F$, and for a given $e_h$, I would like to find the value of $e_f$ that maximises $g$. I tried to use the FindMaximum function, but this seems to miss the point where $e_f=e_h$ where the function may be defined and maximised. For example:

FindMaximum[g[10, 1, 1, 5, 10, 0.24, ef], {ef, 0.2}] returns {0., {ef -> 0.2}} and FindMaximum[g[10, 1, 1, 5, 10, 0.24, ef], {ef, 0.3}] returns {0.698102, {ef -> 0.272076}} which is the maximum on the continuous part for $e_f\geq \frac{c}{a-2 \sqrt{b} \sqrt{F}}$. So in both cases, the point $e_f=0.24$ where the global maximum $g(10, 1, 1, 5, 10, 0.24, 0.24)=0.753472$ is missed.

Ultimately, I would like to plot the argmax of $g(e_f)$ as a function of $e_h$ for given values of the other parameters. What's the best way to do this?

Answer 1

First consider the valid region of the parameters eh,ef

cond[a_?NumericQ, b_?NumericQ, c_?NumericQ, w_?NumericQ,F_?NumericQ ] := (ef == eh && ef > c/a) ||ef >= c/(a - 2 Sqrt[b] Sqrt[F]) 
RegionPlot[ cond[10, 1, 1, 5, 10] , {ef, .2, .3} , {eh, 0.23, .28},PlotPoints -> {100, {eh == ef}}, FrameLabel -> Automatic,Prolog -> {Red, Point[{.24, .24}]}]

The plot shows that the point ef==eh==.24 you expect the maximum isn't allowed!

NMaximize evaluates the maximum

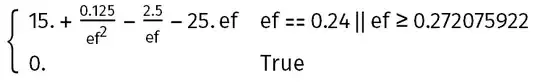
Maximize[g[10, 1, 1, 5, 10, 0.24, ef], ef ]  (*{0.698102, {ef -> 0.272076}}*)

addendum

Obviously Mathematica didn't find the complete valid region. But Maximize is able to solve the problem if you add the constraints ef > 0, eh > 0 and maximize in two dimensions {ef,eh}:

Maximize[{g [10, 1, 1, 5, 10, eh, ef], ef > 0, eh > 0}, {ef, eh}] // N
(*{0.753847, {ef -> 0.242362, eh -> 0.242362}}*)

final addendum

If you are looking for a maximum for given parameters a, b, c, w, F, eh define a region depending on these parameters

reg[a_, b_, c_, w_, F_, eh_] =ImplicitRegion[(ef == eh && ef > c/a) ||ef >= c/(a - 2 Sqrt[b] Sqrt[F]), ef ]

and maximize

NMaximize[ g [10, 1, 1, 5, 10, .24, ef]  , Element[{ef}, reg [10, 1, 1, 5, 10, .24]]] 
(*{0.753472, {ef -> 0.24}}*)

Answer 2

FullSimplify[g[10, 1, 1, 5, 10, 0.24, ef] // N]

I believe these general min/maximize functions use search strategies that start with some initial points, and Mathematica doesn't expect that the max point is located at the isolated point $e_f=0.24$. Therefore, you may need to treat this specially.

Method 1

If[g[10, 1, 1, 5, 10, 0.24, 0.24] > #1,
   0.24, #2[[1, 2]]
   ] & @@ NMaximize[
  FullSimplify[g[10, 1, 1, 5, 10, 0.24, ef]], ef]

0.24

Plot[
 If[g[10, 1, 1, 5, 10, eh, eh] > #1,
    eh, #2[[1, 2]]
    ] & @@ NMaximize[
   FullSimplify[g[10, 1, 1, 5, 10, eh, ef]], ef],
 {eh, 0, 0.5}, PlotRange -> {0, Automatic}]

Method 2

Put the special data together with the result of NMaximize in same format, and then take the largest data according to the first element (value). This is more general.

MaximalBy[
  {
   {g[10, 1, 1, 5, 10, 0.24, 0.24], {ef -> 0.24}},
   NMaximize[FullSimplify@g[10, 1, 1, 5, 10, 0.24, ef], ef]
   },
  First
  ][[1, 2, 1, 2]]

0.24

Plot[
 MaximalBy[
   {
    {g[10, 1, 1, 5, 10, eh, eh], {ef -> eh}},
    NMaximize[
     FullSimplify@g[10, 1, 1, 5, 10, eh, ef], ef]
    }, First
   ][[1, 2, 1, 2]],
 {eh, 0, 0.5},
 PlotRange -> {0, Automatic},
 AxesLabel -> {"\!\(\*SubscriptBox[\(e\), \(h\)]\)", 
\!\(\*UnderscriptBox[\("\<arg max\>"\), 
SubscriptBox[\(e\), \(f\)]]\) g[Subscript[e, h], Subscript[e, f]]}
 ]