Plotting discontinuous functions without spurious vertical segments

Question

Consider the plot of this discontinuous function:

f[x_] := If[2 < x < 3, 0, x]
Plot[f[x], {x, 0, 5}]

I'd like to plot that without the vertical segments. Modifying the function f is not allowed.

ADDED: I should've said more about the restriction on modifying f. In the real application where this came up, f is a messy thing that should be treated as a black box. So we can't pick out the discontinuity, and probably can't invert the function either.

Answer 1

I looked for a way without redefining the function and not using explicit knowledge about it (so it can be generalized)

pl[f_, lims_] := Module[{eps = 0.05},
   Off[InverseFunction::"ifun"];
   Print@Plot[f[u], {u, lims[[1]], lims[[2]]},
      Exclusions ->
       {{f[u] == f[InverseFunction[f][u]], Abs[(f[u] - f[u + eps])] > 10 eps},
        {f[u] == f[InverseFunction[f][u]], Abs[(f[u] - f[u - eps])] > 10 eps}}]
    On[InverseFunction::"ifun"];
   ];

(* Testing *)

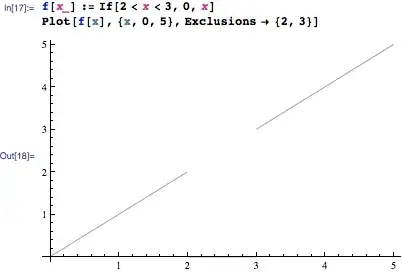
f[x_] := If[2 < x < 3, 0, x];
pl[f, {0, 5}];
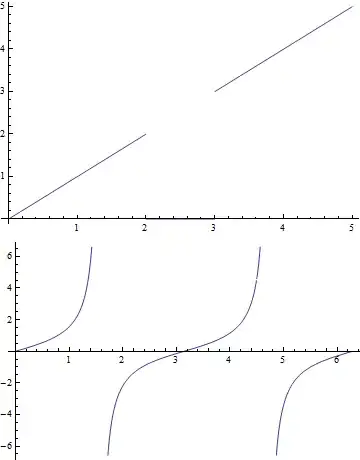
pl[Tan, {0, 2 Pi}]

Edit

Ok, this one does not use InverseFunction, and identifies discontinuities, as far as I tested it:

(*Function Definition*)
pl[f_, lims_]:= Plot[f[u],{u, lims[[1]], lims[[2]]},Exclusions->{True, f[u] == 1}];

(*--------Test--------*)
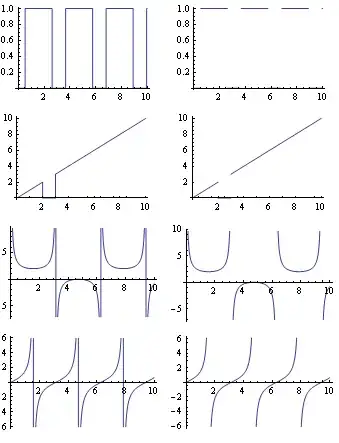
flist = {
   If[Abs@Sin@# > .5, 1, 0] &,
   If[2 < # < 3, 0, #] &,
   1/Sin@# + 1 &,
   Tan};
pk = Table[{Plot[fun[x], {x, 0, 10}], pl[fun, {0, 10}]}, {fun, flist}];
GraphicsGrid[pk]

Here are side by side the results from Plot (without Options) and from this function:

Edit 2

Found a counterexample, and perhaps some comprehension about what is going on there.

   f = If[Abs@Sin@# > .5, 2, 5] &  

Does not work. Why? It's easy ... the discontinuity does not cross f[u]==1 ...

Doing a Reap-Sow on the Plot (as in @rcollyer's answer) I saw that adding the Exclusions with f[u]==1 adds a few points to the trace just around f[u]==1 and seems that that is the trigger for excluding the discontinuities from the domain.

Now trying to find a way to change the f[u]==1 for something that works better ...

Edit 3

Found a way with a discrete derivative, a tricky thing.

Like this:

(*Function Definition*)
pl[f_, lims_]  :=  Plot[f[u], {u, lims[[1]], lims[[2]]},
                              Exclusions -> {(f[u] - f[u + .1])/.1 == 10, 
                                             (f[u] - f[u + .1])/.1 == -10}];  

Note two issues:

1. I had to remove the "True" or "Automatic" option from the Exlusions
2. Taking Abs[] for joining the two Exclusion equalities does not work since it's monitoring the evolution of the lhs ...

Answer 2

The answer is Exclusions as follows:

In this case, your excluding the points where there are discontinuities. It will also accept functional definitions.

Edit: Since you state you can't pick out the exclusions, I assume you mean that unlike the example you gave the exclusions are not known a priori. And, assuming that InverseFunction does not work for you, as per belisarius's solution, then you will have to generate them "by hand". The best bet would be to use EvaluationMonitor to acquire the points Plot uses, like in the example

data = Reap[Plot[Sin[x], {x, 0, 2 Pi}, EvaluationMonitor :> Sow[{x, Sin[x]}]] ][[-1, 1]]

and compare the numerical derivatives on both sides of each point

der = (Subtract@@#[[All,2]])/(Subtract@@#[[All,1]])
Select[Partition[data, 3, 1], Abs[ der@#[[{1,2}]] - der@#[[{2,3}]] ] > tol& ]

where the difference exceeds some tolerance. You'll need to then pull out the offending point, but it should be the only one that exists in 3 consecutive sublists. This then gives you your exclusions.

Edit, part 2: In the continuing jockeying for the "correct" solution to this, I found in the Applications section of the Plot documentation a method that is effective for all of the inital tests used by @belisarius: Exclusions -> {1/f[x] == 0}, and Exclusions -> {1/D[f,x] == 0} works for my pathological example of Sin[1/x^2]. Unfortunately, both still fail for If[Abs@Sin@# > .5, 2, 5]&. Additionally, the use of the derivative fails for all of the initial tests and spuriously removes pieces when combined with 1/f[x]==0.

Answer 3

This works:

f[x_] := Piecewise[{{x, x < 2}, {0, x < 3}, {x, x > 3}}]
Plot[f[x], {x, 0, 5}]

and you also have the advantage that Piecewise is derivable (see docs).

EDIT: But if you can not change f, then you can do this:

Plot[ f[x], {x, 0, 5}, Exclusions -> {2, 3} ]

Answer 4

As pointed out by Wolfram, the following will also work. Not as powerful as Exclusions or Piecewise, of course:

f[x_] := If[2 < x < 3, 0, x]
Plot[f[x], {x, 0, 2, 3, 5}]

Update: This code might have worked in earlier versions of Mathematica. As of version 11, it does not work anymore.

Answer 5

To answer your original question, (I assume you have your reasons for not using the Piecewise solution given by gdelfino)

f[x_]:=If[2<x<3,0,x]
Plot[f[x],{x,0,5},Exclusions->{2,3}]

Answer 6

Maybe I am getting late here, but in Mathematica 11 (and perhaps earlier versions) the ExclusionsStyle option would do the job, also for arbitrary functions...

f[x_] := If[2 < x < 3, 0, x]
Plot[f[x], {x, 0, 5}, ExclusionsStyle -> None]

Another example that also works

f[x_] := Tan[x]
Plot[f[x], {x, 0, 2 \[Pi]}, ExclusionsStyle -> None, PlotRange -> {-20, 20}]

Answer 7

This definitely comes late, but I think another elegant solution is to use in place of Plot[f[x], {x, 0, 5}] the instruction

DiscretePlot[f[x], {x, 0, 5, 0.1}, PlotStyle -> "LineColor" -> None]

I know it doesn't exactly answer the question, but for illustrative purposes it may be more than enough. For functions defined via NIntegrate[] and not known in closed form, moreover, all the above solutions fail because conditions like Exclusions -> {1/f[x] == 0} do not work.