I would like to plot the blue deformed squared pattern rubber sheet surface like in this plot:
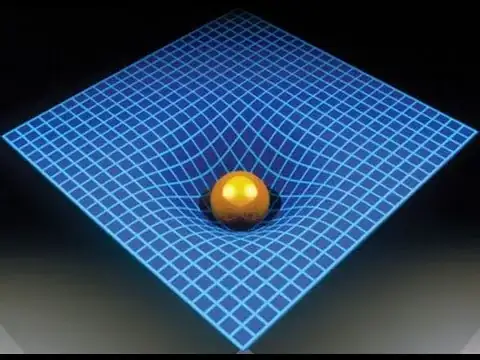
https://physics.stackexchange.com/q/308295/14282
in Mathematica, with the modification that the ball or weight is concentrated in a single point with close or equal to zero volume. Also I would like to plot several weights on the same rubber sheet, and then be able to retrieve the depth or $z$-coordinate, as well as the the given $x$ and $y$ coordinates.
Ultimately I am interested in how this relates to the Travelling Salesman Problem, because I have had the vague idea that given a set of points, say 10 or 20 points each of equal mass/weight, on a rubber sheet one would get a natural sorting of the points by their $z$-coordinates and thereby a solution to the travelling salesman problem.
The $x,y$-coordinates should be considered stationary as if the pointwise weigths are glued to the rubber sheet.
I don't know how to tag this, but I am adding differential equations since I believe it has something to do with it.

DistanceTransformwith a suitable distance function. – C. E. Jul 01 '20 at 13:12