How to plot a figure like this

Question

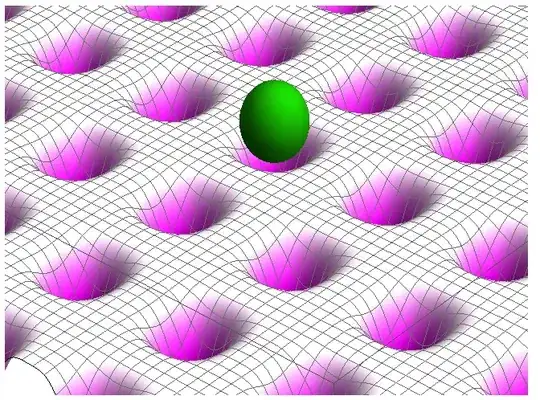
I saw a beautiful figure illustrating the optical lattice clock, and would like to make a similar one.

This is the figure (taken from here)

enter image description here

Is it possible to make a similar one using Mathematica?

Here is my try:

Show[
 Plot3D[0.05 (Cos[3 x] Cos[
       3 y])^4, {x, -\[Pi], \[Pi]}, {y, -\[Pi], \[Pi]}, 
  PlotRange -> {All, All, {-0.1, 0.1}}, PlotPoints -> 200, Mesh -> 60,
   MeshStyle -> Gray, 
  ColorFunction -> (ColorData["GreenPinkTones"][0.5 #3 + 0.5] &)],
 Graphics3D[{Darker[Green], 
   Scale[Sphere[{0, 0, -0.5}], 
    0.25 {\[Pi]/3, \[Pi]/3, .1}, {0, 0, 0}]}, Lighting -> "Neutral"],
 ImageSize -> {651.1743427005708`, 484.8`}, Lighting -> "Neutral", 
 Method -> {"RotationControl" -> "Globe", 
   "RotationControl" -> "Globe"}, 
 PlotRange -> {All, All, {-0.1`, 0.1`}}, 
 PlotRangePadding -> {Automatic, Automatic, Automatic}, 
 ViewAngle -> 0.13079882249358044`, 
 ViewCenter -> {{0.5`, 0.5`, 0.5`}, {0.5218420229698426`, 
    0.6543497570242808`}}, 
 ViewPoint -> {-2.144844931539977`, 
   1.84186142553857`, -1.8593511526229505`}, 
 ViewVertical -> {0.`, 0.`, -1.`}]

enter image description here

Urrmmm. The question was whether it was possible to draw such a picture in Mathematica, and you answer it yourself by drawing it. What kind of additional answers do you expect? — Sjoerd C. de Vries, Nov 30 '13 at 21:55
@SjoerdC.deVries maybe beautiful shadows, focus with fade out, nice colors, textures... :) But I believe that to do what xslittlegrass wants, he has to go to a render program like Unit3D or something equivalently. — Murta, Nov 30 '13 at 22:06
@Murta Indeed. Mathematica has no built-in cast shadows. It can be simulated as shown here.Same with focus, which could be simulated with image blurring. — Sjoerd C. de Vries, Nov 30 '13 at 22:22
Your reference image was probably produced by a renderer with more features than Mathematica's, given the the shadows and depth of field, though they could have been faked. If you are interested in producing "pretty" 3D renderings I think you should consider exporting to an external renderer such as POVray. (Old school.) — Mr.Wizard, Dec 01 '13 at 11:34

Kuba · Accepted Answer · 2013-11-30T23:22:19.230

My pc is rather old so there was not much I could do. Maybe no as pretty as in the link but I'm happy because of the result:

r = 35;
p = Show[
     Plot3D[-Sum[2 Exp[-((x - xo)^2 + (y - yo)^2)], {xo, -24, 8, 4}, {yo, -28, 8, 4}],
            {x, -r, r - 4}, {y, -r, r - 4}, Evaluated -> True, 
            PlotRange -> All, PlotPoints -> 200, Mesh -> 300, ImageSize -> 800,
            ColorFunction -> (Blend[{White, White, White, Purple}, -#3] &), 
            ColorFunctionScaling -> False, MeshStyle -> Directive[Thick, GrayLevel@.4]
           ],
     Graphics3D[{Specularity[White, 15], Green, Sphere[{{-4, -4, .2}, {4, 4, .2},
                                                        {0, 8, .2}}, 1]}
           ],
     BoxRatios -> Automatic, Boxed -> False, Axes -> False, Lighting -> "Neutral",     
     ViewVector -> {{10, 20, 11}, {0, 0, 0}}, ViewAngle -> .5];

p = ImageResize[Rasterize[p, "Image", ImageResolution -> 3 72], Scaled[1/3]]

manual blurring :)

Table[ImageTake[p, {799 - i, 800 - i}, All] ~ Blur ~ (i/100),
      {i, 0, 798,2}] // Reverse // Transpose[{#}] & // ImageAssemble

enter image description here

I decided to not play with shadows because there is no easy way and my pc nearly died :)

Hi Cuba, nice job as always.Which environment do you think the original picture got created? — Alex, Nov 30 '13 at 23:35
@Alex Hello, thank you :) I have no idea, I have no experience with graphics/visualisations software :) — Kuba, Nov 30 '13 at 23:40

score 14 · Answer 2 · edited Nov 30 '13 at 23:24

14

I noticed in the original picture that the raster looks like it's painted on a rubber membrane which is stretched. You can create this effect by using Texture:

img = Image[
   Graphics[
    {
     Blue, Thickness[0.001],
     Table[Line[{{i, 0}, {i, 100}}], {i, 0, 100, 1}],
     Table[Line[{{0, i}, {100, i}}], {i, 0, 100, 1}]
    }, PlotRangePadding -> 0
   ], ImageSize -> 2000, ImageResolution -> 2000];

Show[
 ParametricPlot3D[
  {u, v, -2 Cos[2 u]^4 Cos[2 v]^4}, {u, 0.25 \[Pi], 3.25 Pi}, {v,0.25 \[Pi], 3.25 \[Pi]}, 
  PlotStyle -> Directive[Specularity[White, 100], 
  Texture[img]],
  TextureCoordinateFunction -> ({#1, #2} &), 
  Lighting -> "Neutral", Mesh -> None, PlotRange -> All, 
  PlotPoints -> 300, 
  Boxed -> False, Axes -> None],
 Graphics3D[
   {Green, Sphere[{#1 \[Pi]/2, #2 \[Pi]/2, 0.2}, .5] & @@@ 
             RandomChoice[Flatten[Table[{i, j}, {i, 5}, {j, 5}], 1], 10]
   }], 
   ImageSize -> 1200, ViewPoint -> {1/2, 1/2, 1/2}
 ]

Mathematica graphics

enter image description here

edited Nov 30 '13 at 23:24

Kuba

136,707
13
279
740

answered Nov 30 '13 at 23:07

Sjoerd C. de Vries

65,815
14
188
323

Nice "mesh" :). – Kuba Nov 30 '13 at 23:13
@kuba Thanks, I'm less satisfied with the way Mathematica draws the spheres. The highlight boundaries are too irregular for my taste. – Sjoerd C. de Vries Nov 30 '13 at 23:16
Yes, OP's spheres are more realistic. I've added blurring using my code, feel free to revert it :) – Kuba Nov 30 '13 at 23:23
I was thinking about ImageEffect with "PoissonNoise" too. – Kuba Nov 30 '13 at 23:40
@Sjoerd +1 Very nice! You can improve rendering of the spheres by adding undocumented option Method -> {"SpherePoints" -> 100} to Show. – Alexey Popkov Dec 01 '13 at 08:09
@AlexeyPopkov This in fact is documented :) graphics3D/options/method/3rdexample. But there are other methods too that I don't remember. – Kuba Dec 01 '13 at 08:13
1

@Kuba Thanks, did not notice that. Additional information is available on the bottom of the tutorial/ThreeDimensionalGraphicsPrimitives page and here. – Alexey Popkov Dec 01 '13 at 08:18
@AlexeyPopkov oh yes, thanks, I knew I've seen them somewhere ;) – Kuba Dec 01 '13 at 08:20
@AlexeyPopkov A useful option indeed. – Sjoerd C. de Vries Dec 01 '13 at 15:31
Sjoerd, congratulations on the Steward badge. That's a lot of reviewing. Thank you! – Mr.Wizard Dec 24 '13 at 12:45
@mr.wizard Thanks! There are badges easier earned than this one. It took about a year of checking in a couple of times per day to review anything new in the queue. Having to make sometimes unpopular decisions, and all this while not protected by anonymity. – Sjoerd C. de Vries Dec 24 '13 at 13:23
Your work didn't go unnoticed even before the badge, but it certainly reminded me of just how much work you put in. :-) – Mr.Wizard Dec 24 '13 at 13:27
@Mr.Wizard Not that I care that much about badges, but last year has been rather busy and eventful for me and reviewing has been a way to keep on contributing to the site. – Sjoerd C. de Vries Dec 24 '13 at 13:42

score 0 · Answer 3 · answered Jul 20 '15 at 20:41

0

Would n't the simple egg-crate suffice?

Plot3D[- Sin[x]^4 Sin[y]^4, {x, -3 Pi, 3 Pi }, {y, -2 Pi, 2 Pi },
PlotRange -> {-5, 5}, Mesh -> {80, 80}, Axes -> None, Boxed -> False, PlotStyle -> Yellow]

answered Jul 20 '15 at 20:41

Narasimham

3,160
13
26

How to plot a figure like this

3 Answers3

Linked