How *does* Mathematica generate ticks and tick values?

Question

This question has sort of been asked before in various guises (e.g. here and here), but the answers given there do not answer the question I'm posing.

Before I pose my question, a definition. Let use the name 'ticks definition' for the following information: the locations of the minor ticks, the locations of the major ticks, which major ticks get a label, and which label they get. A ticks definition can be given as a list whose typical entry might look like this: {-0.4, "-0.4", {0.01, 0}, {}}. Each axis gets its own ticks definition. (The entries may also contain information about the lengths and widths of the tick marks, but let's ignore those.)

Now I can pose my question:

In 2D plots generated by the Plot command with the default settings, what function does Mathematica use to generate the ticks definitions? The answer should ideally be a (presumably undocumented) Mathematica function resembling Charting`ScaledTicks (but that particular one doesn't actually produce the same ticks definitions as Plot does with default settings; see below). In other words, the answer should ideally be a function which, given only the x-range and y-range of the plot as inputs,¹ generates the same ticks definitions as the command Plot does by default. When I say 'generate', I mean that the output of such a function should be a list whose entries have the form I mentioned in the previous paragraph. For example, the undocumented function Charting`ScaledTicks produces a list whose typical entry looks like this: {{-4., -4, {0.01, 0.}, {AbsoluteThickness[0.1]}} This is of the right form. However, in the example below, the particular numerical values that Charting`ScaledTicks produces do not reproduce the default behavior of Plot.)

^{1The x-range and y-ranges of the plot can be generated through PlotRange, which is another undocumented function (though this apparently won't work if the plot has certain non-default features, such as a legend).}

If no one knows what this function is, also acceptable would be a function that produces such a string given the entire plot as input (like AbsoluteOptions does—unfortunately, that function does not work correctly in general, see below). In other words, also acceptable would be a function that 'extracts' the tick marks and tick labels from the plot. The question posed here asked for precisely such a function, but none of the answers given there actually work correctly (i.e. reproduce the default behavior of Plot), including the accepted one.

The default behavior of Plot as far as the ticks is not reproduced by any function known to me

One might think that the function I'm looking for would be one (or more) of the following: 1. the output of AbsoluteOptions, or 2. of the LinTicks function from SciDraw, or 3. of the undocumented function Charting`FindTicks, or 4. of the undocumented function Charting`ScaledTicks. However, as will be seen, none of these can reproduce the default behavior reliably. True, for some special values of x-ranges and y-ranges, some of these functions may happen to reproduce the default behavior. However, in the specific example below, none of them do.

^{This of course presents a problem: even if a function is found that reproduces the default behavior in this particular case, how will we know that it would reproduce it in all cases? I suppose this can only be known by someone who actually has access to the source code for the relevant aspect of the Plot command. Nevertheless, if anyone has a guess as to which function is used by Plot, and that function indeed reproduces the default behavior in the example below, that would be of great interest.}

An MWE that shows that the default behavior of Plot is not reproduced by any of the four methods I mentioned

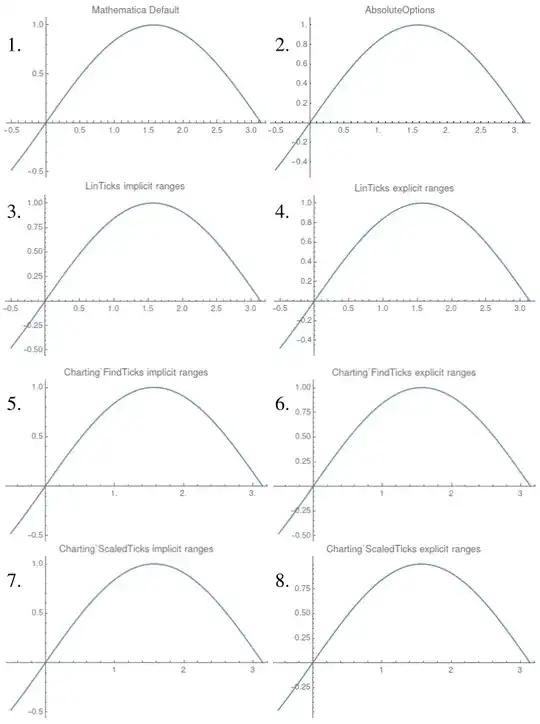
Below, I give a MWE that shows that the default ticks definitions used by Plot are not reproduced via either 'extracting' them by using AbsoluteOptions, or via generating them by using any of the following functions: SciDraw's function LinTicks, the undocumented function Charting`FindTicks, or the undocumented function Charting`ScaledTicks. Namely, I compare the plots in which the ticks were generated using

1. the default Mathematica settings;
2. AbsoluteOptions;
3. the LinTicks function from SciDraw, with the ranges given implicitly (i.e. Ticks -> {LinTicks, LinTicks});
4. as above, but with the ranges explicitly specified (i.e. Ticks -> {LinTicks@@xPlotRange, LinTicks@@yPlotRange}, where {xPlotRange, yPlotRange} = PlotRange[plot]);
5. the undocumented internal function Charting`FindTicks, with the ranges given implicitly;
6. as above, but with the ranges explicitly specified;
7. the undocumented internal function Charting`ScaledTicks, with the ranges given implicitly;
8. as above, but with the ranges explicitly specified;

The point is that none of the methods 2-8 replicate the default in 1 for both axes (see the plots at the end). Thus, Mathematica must be using some other undocumented function to generate the ticks definitions.

(An additional question is why it matters whether the ranges are given implicitly or explicitly, in other words, why 3 doesn't match 4, 5 doesn't match 6, and 7 doesn't match 8.)

I should emphasize that what I am really interested in is an 'explicit' method (like in 4, 6, and 8), which generates an explicit ticks definition (i.e. a list whose entries have a form such as {-0.4, "-0.4", {0.01, 0}, {}}).

Here is the MWE:

(* The default plot *)
plot = Plot[Sin[x], {x, -0.5, Pi}, PlotLabel -> "Mathematica Default"]
(* Extract the plot ranges *)
{xPlotRange, yPlotRange} = PlotRange[plot];
(* Plot using AbsoluteOptions *)
Plot[Sin[x], {x, -0.5, Pi},  Ticks -> {AbsoluteOptions[plot, Ticks][[1, 2, 1]], 
AbsoluteOptions[plot, Ticks][[1, 2, 2]]}, PlotLabel -> "AbsoluteOptions"]
(* Plot using LinTicks with the ranges implicit *)
Plot[Sin[x], {x,-0.5, Pi}, Ticks -> {LinTicks, LinTicks}, PlotLabel -> "LinTicks implicit ranges"]
(* Plot using LinTicks with explicitly specifying the ranges *)
Plot[Sin[x], {x,-0.5, Pi}, Ticks -> {LinTicks@@xPlotRange, LinTicks@@yPlotRange}, PlotLabel -> "LinTicks explicit ranges"]
(* Plot using ChartingFindTicks with the ranges implicit *) Plot[Sin[x], {x,-0.5, Pi}, Ticks -> {ChartingFindTicks[{0, 1}, {0, 1}], 
ChartingFindTicks[{0, 1}, {0, 1}]}, PlotLabel -> "ChartingFindTicks implicit ranges"]
(* Plot using ChartingFindTicks with explicitly specifying the ranges *) Plot[Sin[x], {x,-0.5, Pi}, Ticks -> {ChartingFindTicks[{0, 1}, {0, 1}]@@xPlotRange, 
ChartingFindTicks[{0, 1}, {0, 1}]@@yPlotRange}, PlotLabel -> "ChartingFindTicks explicit ranges"]
(* Plot using ChartingScaledTicks with the ranges implicit *) Plot[Sin[x], {x,-0.5, Pi}, Ticks -> {ChartingScaledTicks[{Identity, Identity}], 
ChartingScaledTicks[{Identity, Identity}]}, PlotLabel -> "ChartingScaledTicks implicit ranges"]
(* Plot using ChartingScaledTicks with explicitly specifying the ranges *) Plot[Sin[x], {x,-0.5, Pi}, Ticks -> {ChartingScaledTicks[{Identity, Identity}]@@xPlotRange, 
ChartingScaledTicks[{Identity, Identity}]@@yPlotRange}, PlotLabel -> "ChartingScaledTicks explicit ranges"]

Here are the plots that the MWE produces in Mathematica 11.3.0.0 running on 64-bit Linux (kubuntu 20.04):

Again, none of the methods are successful in replicating the default behavior for both axes. Indeed, not a single 'explicit' method (which is what I'm after) reproduces the default behavior for the y-axis.