Creating overlapping histogram plots

Question

I am plotting two histograms on the same graph:

g1 = Histogram[bc, ChartStyle -> {Red}]
g2 = Histogram[bcx]
Show[g1, g2, PlotRange -> {{0.1, 0.6}, All}]

enter image description here

But I would like the plots to overlap so that they are "see-through" and I can compare them. I've been trying with

ChartStyle -> {"Overlapped"}

which hasn't been working.

Mr.Wizard · Answer 1 · 2017-05-21T06:04:48.810

31

Doesn't Histogram do this already?

data1 = RandomReal[NormalDistribution[0, 1], 500];
data2 = RandomReal[NormalDistribution[1, 1.5], 500];

Histogram[{data1, data2}]

Mathematica graphics

Version 7 doesn't have HistogramDistribution as shown by Andy Ross. Here is an alternative:

Histogram[{data1, data2},
  BaseStyle  -> FaceForm[None],
  ChartStyle -> {EdgeForm[{Thick, Red}], EdgeForm[{Thick, Blue}]}
]

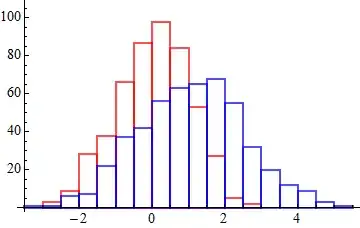
Mathematica graphics

jmlopez asked for a method without the vertical lines. Here is one. The replacement may be a bit fragile. Andy's method is safer for version 8 users.

Update: modified to work in Mathematica 10 as well.

h =
 Histogram[{data1, data2},
   ChartStyle -> (Directive[#, AbsoluteThickness[3]] & /@ {Red, Blue}),
   PerformanceGoal -> "Speed"
 ];

h2 =
 Histogram[{data1, data2},
   ChartStyle -> {{Red, Blue}, Directive[Opacity[0.1], EdgeForm[]]}
 ];

hline = h /. rec : {({{_Rectangle}} | {}) ..} :>
  Line[  Flatten[rec, 2] /. _[{x_, y_}, {X_, Y_}, ___] :> Sequence[{x, Y}, {X, Y}]  ];

Show[hline, h2]

Mathematica graphics

kjo pointed out that my method fails when bars have a height of zero. The simplest fix I can think of is to avoid zero-height bars (which are not drawn, the source of the problem) by using a small offset value for the hspec function.

hfn = $MachineEpsilon + #2 &;

h = Histogram[{data1, data2}, {0.1}, hfn, 
  ChartStyle -> (Directive[#, AbsoluteThickness[3]] & /@ {Red, Blue}), 
  PerformanceGoal -> "Speed"]

h2 = Histogram[{data1, data2}, {0.1}, hfn, 
  ChartStyle -> {{Red, Blue}, Directive[Opacity[0.1], EdgeForm[]]}]

hline = h /. 
   rec : {({{_Rectangle}} | {}) ..} :> 
    Line[Flatten[rec, 2] /. _[{x_, y_}, {X_, Y_}, ___] :> Sequence[{x, Y}, {X, Y}]];

Show[hline, h2]

edited May 21 '17 at 06:04

answered Feb 24 '12 at 22:06

Mr.Wizard

271,378
34
587
1,371

Is there a way to get rid of the middle lines? And get something like this on the second example. I like how they just set the Apperance to Transparent and its done. – jmlopez Jun 04 '12 at 22:47
3

I feel that it is a little absurd how there is tons of examples of how to use Histogram and yet there is no option to do what you just did in the update. All it really is is a line plot connecting points with the fill axis property. Anyway, thank you Mr. Wizard. – jmlopez Jun 05 '12 at 07:46
1

There's a problem with the histogram outlining scheme at the end (last plot), when the histogram contains empty bins (not an uncommon situation, especially towards the tails). To elicit this condition, just add a narrow bin width specification (e.g. {0.1}) as a second argument to the Histogram expressions. – kjo May 18 '17 at 18:01
1

@kjo I think I found a relatively simple fix; please take a look and test it for me. – Mr.Wizard May 21 '17 at 06:03
Your fix is very elegant I think, and it works beautifully. A couple of thoughts. Since the offset added by the hspec function (hfn) is so small, one could omit it from the second histogram (h2). In fact, if one has some time to kill, one could even set hfn = offset + #2 &, for some arbitrary positive integer offset, and then change the last subexpression in hline from Sequence[{x, Y}, {X, Y}] to Sequence[{x, Y - offset}, {X, Y - offset}]. (A probably useless embellishment.) – kjo May 23 '17 at 12:18

score 22 · Answer 2 · answered Feb 25 '12 at 05:56

You also have the option of SmoothHistogram.

data1 = RandomVariate[NormalDistribution[0, 1], 10^3];
data2 = RandomVariate[NormalDistribution[.4, 1], 10^3];

SmoothHistogram[{data1, data2}, 
 PlotStyle -> {{Thick, Red}, {Thick, Blue}}]

enter image description here

Or using one of the nonparametric distributions HistogramDistribution...

Plot[Evaluate[{PDF[HistogramDistribution[data1], x], 
   PDF[HistogramDistribution[data2], x]}], {x, -4, 4}, 
 Exclusions -> None, PlotPoints -> 100, 
 PlotStyle -> {{Thick, Red}, {Thick, Blue}}]

enter image description here

score 21 · Accepted Answer · edited Jun 16 '20 at 09:23

21

First method

You could make the one in front partially transparent:

bc = RandomVariate[NormalDistribution[], 1000];
bcx = RandomVariate[NormalDistribution[], 1000];
g1 = Histogram[bc, ChartStyle -> {Red}];
g2 = Histogram[bcx, ChartStyle -> {Directive[Blue, Opacity[.5]]}];
Show[g1, g2, PlotRange -> All]

Mathematica graphics

Direct method

The same effect can be achieved by plotting the two distributions in the same plot directly:

Histogram[{bc, bcx}, ChartStyle -> {Red, Blue}]

edited Jun 16 '20 at 09:23

Community

1

answered Feb 24 '12 at 19:18

Heike

35,858
3
108
157

1

Why lead with the more complex solution?! – Brett Champion Feb 24 '12 at 21:54
2

@BrettChampion the second one didn't occur to me until after I finished writing the more complex solution. – Heike Feb 24 '12 at 21:59

Tim Mayes · Answer 4 · 2012-02-24T23:19:37.577

4

For g2 you should be able to change the definition to:

g1 = Histogram[bcx, ChartStyle -> Opacity[0.50, Blue]]

To get the front histogram to be more transparent. Fiddle around with the 0.50 to get it to look the way that you want.

edited Feb 24 '12 at 23:19

answered Feb 24 '12 at 19:21

Tim Mayes

1,449
2
14
18

Creating overlapping histogram plots

4 Answers4

First method

Direct method

Linked