14

This question asks to find the largest circle within a convex polygon, specifically this one:

Graphics[
 {Line[{{0,1}, {0,6}, {4,10}, {8,10}, {11,7}, {11,4}, {7,0}, {1,0}, {0,1}}]}
]

enter image description here

One can optimize over the $(x,y)$ location of its center maximizing its radius $r$, but this seems quite a non-Mathematica approach. Presumably there is a method based on RegionFunctions, Centroids, and such to exploit Mathematica's region functionality.

Alas, the natural primitives such as Centroid and all the RegionMeasures and RegionMemberQ I could think of didn't help.

I have a feeling there is a one-line solution to this, but cannot find it. It would be especially great to get an analytic solution (based on the equations of the polygon edges, say), rather than just some numerical center location and radius.

J. M.'s missing motivation
  • 124,525
  • 11
  • 401
  • 574
David G. Stork
  • 41,180
  • 3
  • 34
  • 96
  • 1
    I think the answers here might be helpful. I get a good result using inCircle from this answer. – Jason B. Oct 06 '20 at 01:19
  • Partly related too https://mathematica.stackexchange.com/q/226058/72682 though the method there was to test random seed points and ovoid other obstacles packing the interior. – flinty Oct 06 '20 at 01:21
  • I wouldn't be so certain it will be a one-liner. Looking at this site I'm struck by this sentence: "the solution will contact three edges". That seems true, but I can't say for sure. But if it is true - finding the incircle of a triangle is easy and analytic. Just find the incircle for all sets of three edges, and grab the largest one. – Jason B. Oct 06 '20 at 01:52
  • The solution disk must touch at least three edges of the convex polygon. If the two touched sides are not parallel, one can always displace the disk one of the two candidate directions to enable a larger radius. In the (rare) case the touched sides are parallel (as in a long rectangle), then one can shift the solution one direction until it touches one of the remaining sides (even though it does not change the solution area). – David G. Stork Oct 06 '20 at 01:55
  • @DavidG.Stork Very nice problem. Perhaps there exists a unique "minimal" solution with minimal distance between the centroids of disk and polygon? – Ulrich Neumann Oct 06 '20 at 08:37
  • Maybe this answer by Carl Woll helps? https://mathematica.stackexchange.com/a/164862 – Henrik Schumacher Oct 06 '20 at 10:19

5 Answers5

14
poly = Polygon @ {{0, 1}, {0, 6}, {4, 10}, {8, 10}, {11, 7}, {11, 4}, 
   {7, 0}, {1,  0}, {0, 1}};

dsk = Disk[{x, y}, r];

We can use RegionWithin[poly, dsk] as the constraint in ArgMax:

sol = Quiet @ ArgMax[{r, RegionWithin[poly, dsk]}, {x, y, r}] 

{43/8, 39/8, 13/(2 Sqrt[2])}  

Graphics[{EdgeForm[Black], FaceForm[Yellow], poly, 
   Red, Circle[Most @ sol, Last @sol], PointSize[Large], Point[Most @ sol]}]

enter image description here

kglr
  • 394,356
  • 18
  • 477
  • 896
  • Great, that's the one-liner ! I tried numerically NArgMax[{ r, RegionWithin[poly, dsk]}, {x, y, r}] but MMA doesn't evaluate. Any idea? Thanks. – Ulrich Neumann Oct 06 '20 at 08:00
  • @UlrichNeumann, I also tried NArgMax and NMaximize and had to abort because it was taking too long. I don't know why. – kglr Oct 06 '20 at 08:20
  • Mystery MMA... Thanks! – Ulrich Neumann Oct 06 '20 at 08:32
  • 3
    Yep... that counts as a one-liner! I certainly didn't know about RegionWithin. Once again the mysterious kglr solves what few others can. ($\checkmark$) – David G. Stork Oct 06 '20 at 15:58
  • @kglr I'm wondering , the code sol=... doesn't evaluate anymore in Mathematica v12.2, it only shows ArgMax[...] with several conditions like (Indeterminate | Indeterminate) \[Element] Reals && Indeterminate <= -1 . – Ulrich Neumann Mar 15 '21 at 12:58
  • @UlrichNeumann, thank you for catching this. It looks like 12.2.0 updates broke something. I will see if if it can be fixed. – kglr Mar 15 '21 at 21:08
  • @kglr Thank you for your assistence! – Ulrich Neumann Mar 15 '21 at 22:22
  • @UlrichNeumann, replacing RegionWithin[poly, dsk] with RegionWithin[poly, dsk]/. LessEqual[Indeterminate,_]|Element[Indeterminate|_,_]->True fixes the issue (not sure how robust this is though). – kglr Mar 16 '21 at 09:01
  • @kglr Thank you, some minutes ago I asked for your proposed substitution! – Ulrich Neumann Mar 16 '21 at 09:06
  • You can use DeleteDuplicates@pts to avoid Indeterminate. – chyanog Jun 27 '23 at 09:13
10

As an area maximization problem:

reg = Polygon[{{0, 1}, {0, 6}, {4, 10}, {8, 10}, {11, 7}, {11, 4}, {7, 0}, {1, 0}, {0, 1}}];
rnf = RegionNearest[RegionBoundary[reg]];
gendisk[{x_, y_}] := Disk[{x, y}, EuclideanDistance[{x, y}, rnf[{x, y}]]]
cost[{x_?NumericQ, y_?NumericQ}] := Area[gendisk[{x, y}]]
{err, sol} = NMaximize[cost[{x, y}], {x, y} \[Element] reg,
  Method -> "RandomSearch"];
Graphics[{FaceForm[None], EdgeForm[Black], reg, Yellow, 
  FaceForm[Yellow], gendisk[Values@sol], Red, Point[Values[sol]]}]

disk in convex

There's a ridge at the centre of the distance transform, so I don't think there is a unique solution but a family of disks with maximal area.

ImageAdjust@DistanceTransform@ColorNegate@Graphics[reg]

distance transform

flinty
  • 25,147
  • 2
  • 20
  • 86
  • This is nice, but ultimately equivalent to the general form I considered: Searching through $(x,y)$ while keep $r$ as large as possible. (+1)... but I have a feeling a more elegant solution remains to be shown. – David G. Stork Oct 06 '20 at 01:32
7

In version 13.3, the problem can be solved with InscribedBall

pts = {{0, 1}, {0, 6}, {4, 10}, {8, 10}, {11, 7}, {11, 4}, {7, 0}, {1, 0}, {0, 1}};
Graphics[{Line[pts], Opacity[0.3], InscribedBall@pts}]

![enter image description here

chyanog
  • 15,542
  • 3
  • 40
  • 78
4

I played around a bit with this problem and noticed that all numeric functionalities become significantly faster when you use a polygon with machine-precision points. So if you want to use NMaximize or the like, I highly recommend this.

Furthermore, here's a numerical implementation that uses SignedRegionDistance:

Clear[x];
poly = Polygon @ N[{{0, 1}, {0, 6}, {4, 10}, {8, 10}, {11, 7}, {11, 4}, {7, 0}, {1, 0}, {0, 1}}];
sol = With[{
   sgnDist = SignedRegionDistance[poly]
  },
  NMinimize[sgnDist[x], x \[Element] poly]
]
Graphics[
 {
  {Red, Disk[x /. Last[sol], Abs[First @ sol]]},
  {FaceForm[None], EdgeForm[Black], poly}
 }
]

enter image description here

Sjoerd Smit
  • 23,370
  • 46
  • 75
  • I also test SignedRegionDistance, your approach is best than my original method. – cvgmt Jan 15 '21 at 09:34
  • Thanks (+1). A helpful improvement for larger problems. – David G. Stork Jan 15 '21 at 16:38
  • @DavidG.Stork There are some more optimizations you can make, potentially. For ConvexPolygonQ polygons, you can use FindMinimum using RegionCentroid as an initial guess. That should be faster for more complicated polygons. – Sjoerd Smit Jan 15 '21 at 17:20
3

Test non-convex set

Clear["Global`*"];
pts = {{0, 1}, {0, 6}, {4, 10}, {2, 10}, {11, 7}, {11, 4}, {7, 0}, {1,
     0}};

(* pts = {{0, 1}, {0, 6}, {4, 10}, {2, 10}, {4, 7}, {11, 4}, {7, 0}, {1, 
    0}}; *)
poly = Polygon[pts];
bds = InfiniteLine /@ Partition[pts, 2, 1, 1];
sol = Maximize[{r, 
    Table[RegionDistance[bd, {x, y}] >= r, {bd, bds}], {x, 
      y} ∈ poly}, {r, x, y}] // Simplify
Graphics[{{Opacity[0.2], poly}, Point[{x, y}], Circle[{x, y}, r]} /. 
  Last[sol]]

enter image description here

Conjecture

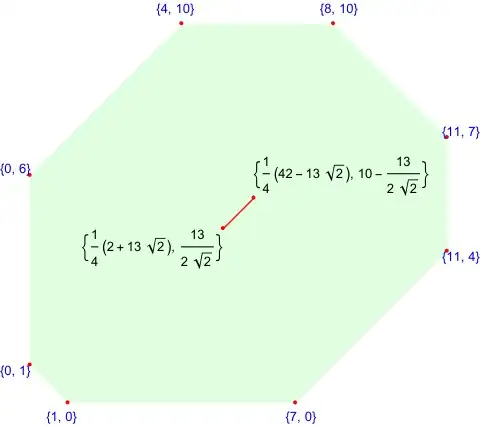
We believe that the center of the max circle should be lie in the line segment.

pts = {{0, 1}, {0, 6}, {4, 10}, {8, 10}, {11, 7}, {11, 4}, {7, 0}, {1,
     0}};
poly = Polygon[pts];
fig1 = Graphics[{{LightGreen, poly}, {Red, Point[pts]}, Blue, 
    Text[#, RegionCentroid[RegionDifference[Disk[#, 1.3], poly]]] & /@
      pts}];
p1 = {x, y} /. (Reduce[
       RegionDistance[InfiniteLine[{{0, 6}, {4, 10}}], {x, y}] == 
         RegionDistance[InfiniteLine[{{7, 0}, {11, 4}}], {x, y}] == 
         RegionDistance[InfiniteLine[{{1, 0}, {7, 0}}], {x, y}] && {x,
           y} ∈ poly, Reals] // ToRules) // Simplify;
p2 = {x, y} /. (Reduce[
       RegionDistance[InfiniteLine[{{0, 6}, {4, 10}}], {x, y}] == 
         RegionDistance[InfiniteLine[{{7, 0}, {11, 4}}], {x, y}] == 
         RegionDistance[
          InfiniteLine[{{4, 10}, {8, 10}}], {x, y}] && {x, 
          y} ∈ poly, Reals] // ToRules) // Simplify;
Show[fig1, 
 Graphics[{Text[p1, p1, {1, 1}], 
   Text[p2, p2, {-1, -1}], {Red, Point[{p1, p2}], Line[{p1, p2}]}}]]

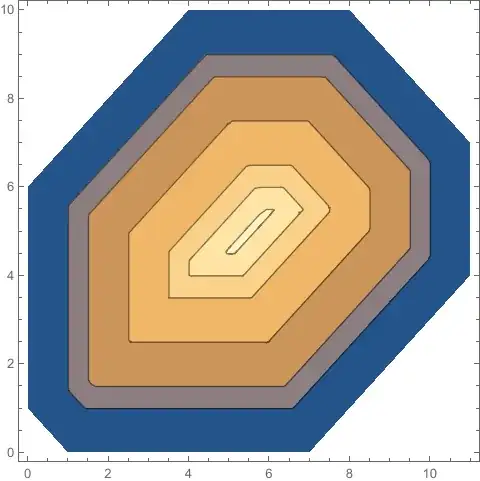
enter image description here

pts = {{0, 1}, {0, 6}, {4, 10}, {8, 10}, {11, 7}, {11, 4}, {7, 0}, {1,
     0}};
poly = Polygon[pts];
bds = InfiniteLine /@ Partition[pts, 2, 1, 1];
Maximize[{Min[RegionDistance[#, {x, y}] & /@ bds], {x, y} ∈ 
     poly}, {x, y}] // Simplify;
ContourPlot[
 Min[RegionDistance[#, {x, y}] & /@ bds], {x, y} ∈ poly, 
 Contours -> {1, 1.5, 2.5, 3.5, 4, 4.5}, ContourShading -> Automatic, 
 PlotPoints -> 50, MaxRecursion -> 2]

enter image description here

Edit II

pts = {{0, 1}, {0, 6}, {4, 10}, {8, 10}, {11, 7}, {11, 4}, {7, 0}, {1,
     0}};
poly = Polygon[pts];
bds = InfiniteLine /@ Partition[pts, 2, 1, 1];
Maximize[{Min[RegionDistance[#, {x, y}] & /@ bds], {x, y} ∈ 
    poly}, {x, y}] // Simplify

$$\left\{\frac{13}{2 \sqrt{2}},\left\{x\to \frac{1}{4} \left(42-13 \sqrt{2}\right),y\to 10-\frac{13}{2 \sqrt{2}}\right\}\right\}$$

pts = {{0, 1}, {0, 6}, {4, 10}, {8, 10}, {11, 7}, {11, 4}, {7, 0}, {1,
     0}};
poly = Polygon[pts];
bds = InfiniteLine /@ Partition[pts, 2, 1, 1];
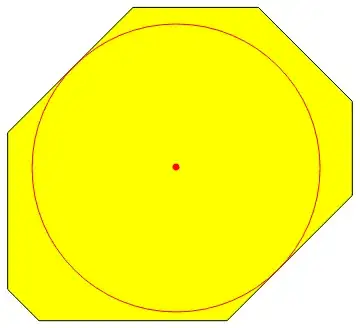
sol = Maximize[{r, 
    Sequence @@ 
     Table[EuclideanDistance[RegionNearest[bd, {x, y}], {x, y}] >= 
       r, {bd, bds}], {x, y} ∈ poly}, {r, x, y}] // Simplify
Graphics[{{Opacity[0.1], poly}, Point[{x, y}], Circle[{x, y}, r]} /. 
   Last[sol]] // Timing

enter image description here $$\left\{\frac{13}{2 \sqrt{2}},\left\{r\to \frac{13}{2 \sqrt{2}},x\to \frac{11}{2},y\to 5\right\}\right\}$$

Edit I

pts = {{0, 1}, {0, 6}, {4, 10}, {8, 10}, {11, 7}, {11, 4}, {7, 0}, {1,
     0}};
poly = Polygon[pts];
bds = InfiniteLine /@ Partition[pts, 2, 1, 1];
sol = Maximize[{r, 
    Table[RegionDistance[bd, {x, y}] >= r, {bd, bds}], {x, 
      y} ∈ poly}, {r, x, y}] // Simplify
Graphics[{{Opacity[0.2], poly}, Point[{x, y}], Circle[{x, y}, r]} /. 
  Last[sol]]

$$\left\{\frac{13}{2 \sqrt{2}},\left\{r\to \frac{13}{2 \sqrt{2}},x\to \frac{43}{8},y\to \frac{39}{8}\right\}\right\}$$

If we add condition to y such as y>=5,the result is

$$\left\{\frac{13}{2 \sqrt{2}},\left\{r\to \frac{13}{2 \sqrt{2}},x\to \frac{355}{64},y\to \frac{323}{64}\right\}\right\}$$

So It must be exist a line attain the maximum.

cvgmt
  • 72,231
  • 4
  • 75
  • 133
  • This is great (+1)... far more than was required by my request for a "one-liner." I knew the solution admitted the circle center being on a line (as can be found by Skeletonization) but your approach is analytic, which is almost always superior. Thanks. – David G. Stork Jan 15 '21 at 19:01