I start with an array of points (cba) and add randomness to generate (cbar). Four point are deleted from it to generate x and a convex hull is generated named chm.
Clear["Global`*"];
SeedRandom[1];
cba = (CoordinateBoundsArray[{{-4, 4}, {-4, 4}}, 1, Center] //
Flatten[#, 1] &) ;
cbar = RandomReal[{-0.25, 0.25}] + # & /@ cba;
x = Complement[cbar, RandomChoice[cbar, 4]];
chm = ConvexHullMesh@cbar;
ListPlot[x
, AspectRatio -> Automatic
, Frame -> True
, Axes -> False
, Epilog -> {FaceForm[Opacity[0.2, Yellow]]
, EdgeForm[Dashed], chm
}
]
Question
How can I identify the emptiest region and put a maximally sized disk there such that no random points are within this disk. The disk also needs to be within the ConvexHullMesh region chm rendered in yellow. Thanks for your help.
This would be similar to 231328 but here I am lacking the polygon and hence the difficulty.

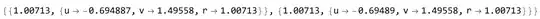

1.00713, ane theMethod -> "DifferentialEvolution"give0.977293. – cvgmt Feb 23 '24 at 06:37{0.977293,{u->-0.645305,v->-1.41163,r->0.977293}}for bothDifferentialEvolutionandRandomSearch. The circle is situated in the other empty space underneath what you have as the solution. It is quite strange. – Syed Feb 23 '24 at 06:55Maximize[dist@{u,v},{u,v}\[Element]chm]get same result – yode Feb 23 '24 at 07:06ris removed. – Syed Feb 23 '24 at 08:01