Visualizing set partition lattice

Question

There's a cool visualization of set of all partition over 4 elements ordered by refinement, which makes it a lattice. Can Mathematica be used to generate these kinds of visualizations automatically? This lattice is used when converting between moments and cumulants, also known as Möbius inversion.

A related question dealt with visualizing individual entries in the lattice -- Generating set partition diagrams

Answer 1

The function refinementQ[x, y] returns True if partition y is a refinement of partition x:

ClearAll[refinementQ, oneElementRefinementQ]
refinementQ[x_, y_] := And @@ (Function[i, Or @@ (SubsetQ[#, i] & /@ x)] /@ y);
oneElementRefinementQ[x_, y_] := And[Length[y] == 1 + Length[x], refinementQ[x, y]]
partitions4 = SortBy[{Length@# &, Min[Length /@ #] &}]@(Sort /@ partition[Range @ 4]);

We can use oneElementRefinementQ with RelationGraph with built-in layout "MultipartiteEmbedding":

RelationGraph[oneElementRefinementQ, partitions4, 
  GraphLayout -> {"MultipartiteEmbedding",  
     "VertexPartition" -> Tally[Length /@ partitions4][[All, -1]]},
  VertexSize -> Large, ImageSize -> 600, 
  EdgeShapeFunction -> "Line", 
  VertexShapeFunction -> (Inset[Framed[
   subsetsPlot["Point", .1, 14, AbsolutePointSize[9], 
         AbsoluteThickness[9]][4, #2], RoundingRadius -> 10, 
       Background -> White], #, {0, 0}, Scaled[.15]] &)]

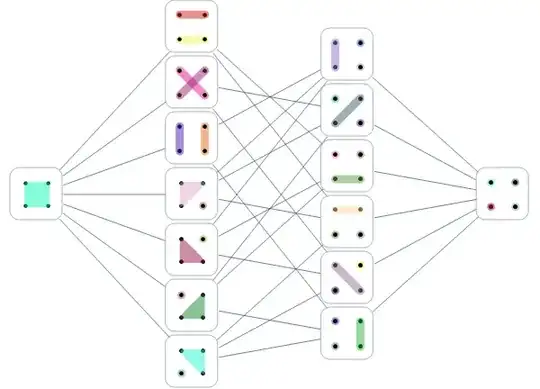
Alternatively, we can use VertexCoordinates with custom coordinates:

vCoords = ScalingTransform[{1, 1/2}]@RotationTransform[-Pi/2]@
    GraphEmbedding[CompleteGraph[Length /@ GatherBy[partitions4, Length]]];
RelationGraph[oneElementRefinementQ, partitions4, 
 ImageSize -> 700, 
 VertexCoordinates -> vCoords, VertexSize -> Large, 
 EdgeShapeFunction -> "Line", 
 VertexShapeFunction -> 
     (Inset[Framed[subsetsPlot[][4, #2], RoundingRadius -> 20, 
        Background -> White], #, {0, 0}, Scaled[.15]] &)]

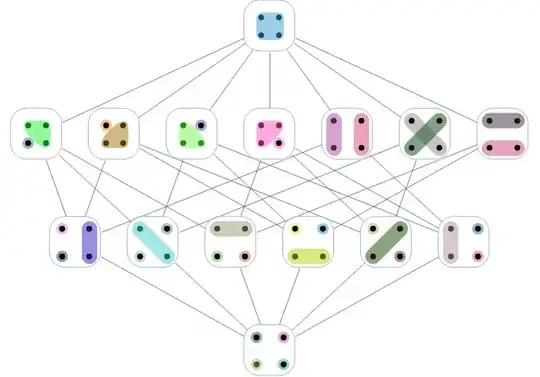
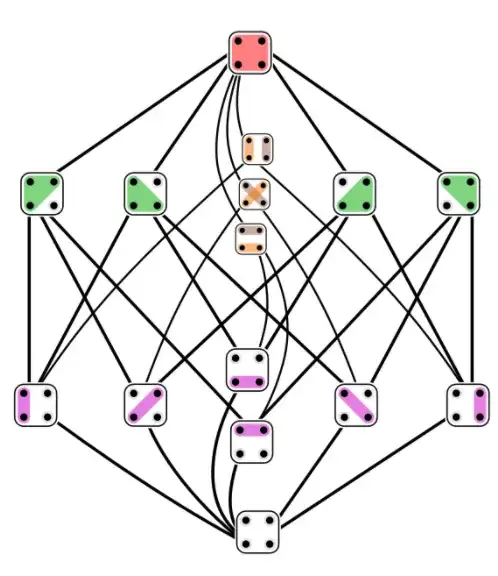
Use vCoords2 instead of vCoords where

vCoords2 = Join @@ MapIndexed[
    Thread[{If[# == 1, {0}, Subdivide[-1, 1, # - 1]], (1 - #2[[1]])/2}] &,
    Length /@ GatherBy[partitions4, Length]]

to get

Replace subsetsPlot[] with subsetsPlot["Text"] to get:

partitions5 = SortBy[{Length@# &, Min[Length /@ #] &}]@(Sort /@ 
     partition[Range@5]);
vCoords = ScalingTransform[{3/2, 1}] @ RotationTransform[-Pi/2]@
    GraphEmbedding[CompleteGraph[Length /@ GatherBy[partitions5, Length]]];
RelationGraph[oneElementRefinementQ, partitions5,

 ImageSize -> 800, VertexCoordinates -> vCoords, VertexSize -> Large, 
 EdgeShapeFunction -> "Line", 
 VertexShapeFunction -> 
      (Inset[Framed[subsetsPlot["Point", .1, 14, AbsolutePointSize[4], 
        AbsoluteThickness[6]][5, #2], RoundingRadius -> 5, 
      Background -> White, FrameMargins -> -5], #, {0, 0}, Scaled[.05]] &)]

Use

vCoords2 = Join @@ MapIndexed[
    Thread[{If[# == 1, {0}, Subdivide[-1, 1, # - 1]], (1 - #2[[1]])/(5 - 2)}] &, 
    Length /@ GatherBy[partitions5, Length]]

instead of vCoords to get

Appendix: Functions from Generating set partition diagrams (subsetsPlot slightly modified):

ClearAll[partition, boX, bloB, subsetsPlot]
partition[{x_}] := {{{x}}}
partition[{r__, x_}] := Join @@ (ReplaceList[#, {{b___, {S__}, a___} :> 
   {b, {S, x}, a}, {S__} :> {S, {x}}}] & /@ partition[{r}])
boX[a : {, _}, e] := a + # & /@ Tuples[{-e, e}, {2}]
boX[a : {{, _} ..}, e] := Flatten[boX[#, e] & /@ a, 1]
bloB[x_, e_] := Switch[Length @ x, 1, Point@x, 2, Line@x, _, 
  FilledCurve[BSplineCurve[#, SplineClosed -> True] & @@ 
    ConvexHullMesh[boX[x, e]]["FaceCoordinates"]]]
subsetsPlot[vshape : ("Point" | "Text") : "Point", size_: .4, 
    ts_: 14, aps_: AbsolutePointSize[15], 
    at_: AbsoluteThickness[20]][n_, subsets_, o : OptionsPattern[Graphics]] := 
 Graphics[{Black, If[vshape == "Text", 
    MapIndexed[Text[Style[#2[[1]], ts], #] &, CirclePoints[n]], 
   {AbsolutePointSize[aps[[1]]/2], Point@CirclePoints[n]}], 
     RandomColor[], Opacity[.5], aps, at, CapForm["Round"], 
     bloB[CirclePoints[n][[#]], size]} & /@ subsets, o, ImagePadding -> 10]