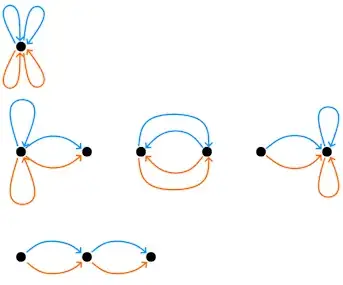
Explanation why some graphs appear more than ones:
It depends on the number of possible paths - some graphs have only one possibility, the graph below has four.

Functions definitions:
I borrowed removeIsomorphicDoublePaths from @Domen's answer.
removeIsomorphicPaths is variation of removeIsomorphicDoublePaths.
edgesTagged adds tags to edge for proper displaying in Graph.
ef is edge shape function.
removeIsomorphicDoublePaths[doublePaths_] :=
Module[{doublePathsFlat, hashes, isoHashes},
doublePathsFlat = Flatten /@ doublePaths;
hashes = ToString@Values[PositionIndex[#]] & /@ doublePathsFlat;
isoHashes = DeleteDuplicates[hashes];
Part[doublePaths, First@FirstPosition[hashes, #] & /@ isoHashes]]
removeIsomorphicPaths[doublePaths_] := Module[{hashes, isoHashes},
hashes = ToString@Values[PositionIndex[#]] & /@ doublePaths;
isoHashes = DeleteDuplicates[hashes];
Part[doublePaths, First@FirstPosition[hashes, #] & /@ isoHashes]]
nk[n_, k_] := n!/((n - k)!)
edgesTagged[e_] := Block[{po, v},
v = {};
If[(po =
Position[Append[Sort[Most@#], Last@#] & /@ v,
Append[Sort@Most[#], {#[[-1, 1]], _}]]) != {},
AppendTo[v, Append[Most[#], Last@v[[(Last@po)[[1]]]] + {0, 1}]],
AppendTo[v, #]] & /@
MapIndexed[Append[#, {1 + Boole[First@#2 > Length[e]/2], 1}] &, e];
Join[Most@#, {Append[Last@#, Subtract @@ Most@#]}] & /@ v
]
arrow = Graphics[{Line[# + {-1, 0} & /@ {{-1, 1}, {1, 0}, {-1, -1}}]}];
ef = ({Thick, (RGBColor /@ {"#FF6B00", "#0094FF"})[[#2[[3,
1]]]], {Arrowheads[{{0.01, 0.5 + 0.01, arrow}}],
Arrow@BSplineCurve[{First@#,
If[#2[[3, 3]] != 0,
Mean@#[[{1, -1}]] + #2[[3, 3]]^2(#2[[3, 1]] - 3/2) {0,
0.4 + 0.2 #2[[3, 2]]/Abs[#2[[3, 3]]]},
Splice[Table[Mean@#[[{1, -1}]],
3] + {{-0.05 - 0.05 #2[[3, 2]], 0.3} + {0,
0.2 #2[[3, 2]]/2}, {0, 0.5} + {0,
0.2 #2[[3, 2]]/2}, {0.05 + 0.05 #2[[3, 2]], 0.3} + {0,
0.1 #2[[3, 2]]}}Table[{1, (#2[[3, 1]] - 3/2)}, 3]]],
Last@#}]}} &);
Code to produce edges for all graphs.
do = 5;
tup = Prepend[#, 1] & /@ Tuples[Range[do], {do - 1}];
gr = GatherBy[#, Last] & /@ {removeIsomorphicPaths[tup], tup};
pairs = Flatten[Tuples /@ Transpose[gr], 1];
jp = Join @@@ Map[Partition[#, 2, 1] &, pairs, {2}];
edges = removeIsomorphicDoublePaths[
Select[jp, AllTrue[Values@Counts[#], EvenQ] &]];
FullSimplify[
Total[nk[n, Flatten[#] // Union // Length]*
Times @@ ((Values@Counts[#] - 1)!!) & /@ edges]] // Apart
48 n + 28 n^2 + 28 n^3 + n^5
Code to display graphs:
Graph[DirectedEdge @@@ #, EdgeShapeFunction -> ef,
VertexStyle -> Black, VertexSize -> Tiny,
VertexCoordinates ->
Table[{n,
0}, {n, #[[All, {1, 2}]] // Flatten // Union // Length}],
ImageSize ->
200*(#[[All, {1, 2}]] // Flatten // Union //
Length)] & /@ (edgesTagged /@ edges) // Column
do=2

do=3

do=4

do=5

image 2
image 3
Some interesting graphs for do=6 out of all 559

And another two interesting graphs for do=6 where there is impossibility of having no crossings of edges.










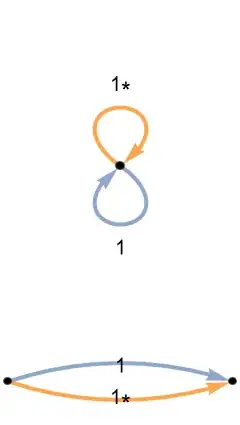



Tr(AAAA)should help with your question ofTr(AAA A'A'A')orTr(AA A'A'). The rules they used are different. You still have not explained why there are four instances of the same graph in hand-drawn image. If we do not know the rules to create these graphs how can we answer the question? – azerbajdzan Mar 26 '24 at 12:53a[i1,i2]a[i2,i3]a[i3,i4]a[i4,i1]/.{i2->i1,i3->i1}which results ina[i1, i1]^2 a[i1, i4] a[i4, i1]which when taking the expectation results in 0 as not all terms have even powers? Am I missing something obvious? – JimB Mar 27 '24 at 23:45