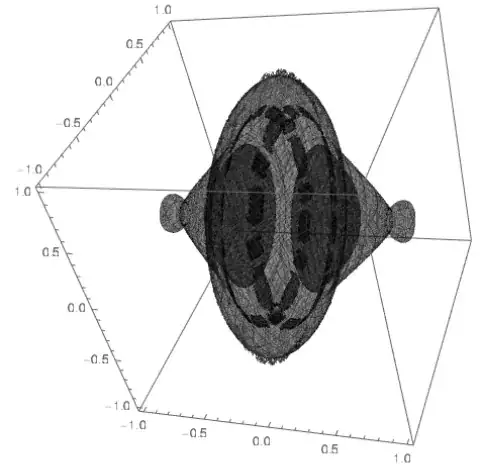
Here's my surface plot of the star showing analytically the magnitude of F(s,t). Note in particular I am summing both real and complex roots. Maybe could use the height to then color-code the 2D plots above.
r[x_, y_] = D[f[x, y], {{x, y}}] // Simplify
theF[{x_,
y_}] := (33 + 24 x^4 - 116 y^2 + 96 y^4 - 78 x^2 + 96 x^2 y^2)/25
mySumFun[s_?NumericQ, t_?NumericQ] := Module[{mySol},
mySol = {x, y} /.
NSolve[{1/5 x (-3 + 2 x^2 + 4 y^2) == s,
1/5 y (-11 + 4 x^2 + 8 y^2) == t}, {x, y}];
Plus @@ ((1/Abs[theF[#]]) & /@ mySol)
];
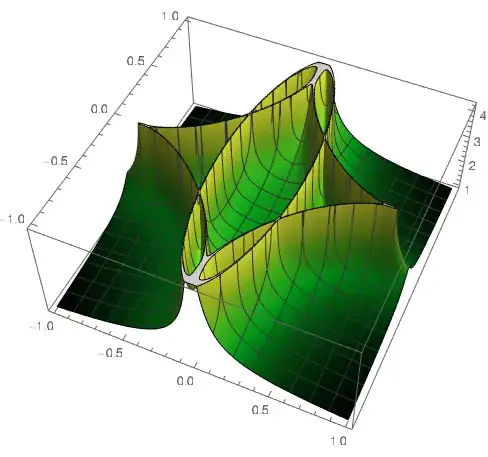
p1 = Plot3D[mySumFun[s, t], {s, -1, 1}, {t, -1, 1}, PlotRange -> 20,
ClippingStyle -> None, BoxRatios -> {1, 1, 1},PlotPoints->100]
GraphicsRow[{p1, p1}]
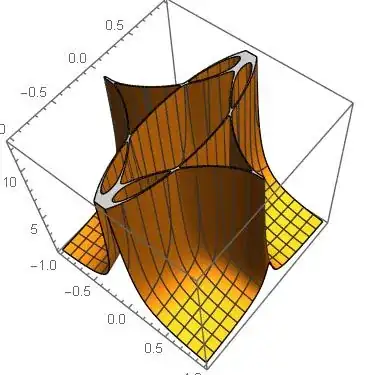
And here is the under-side which looks more like a star. Might be a challenge to remove the four corners and reveal only the imbedded star-shape.
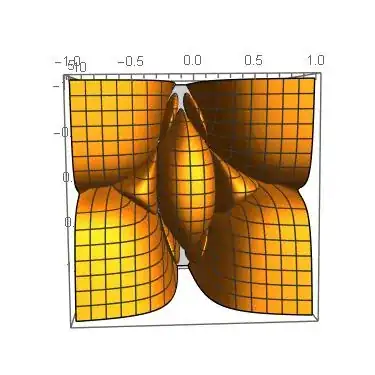
Update:
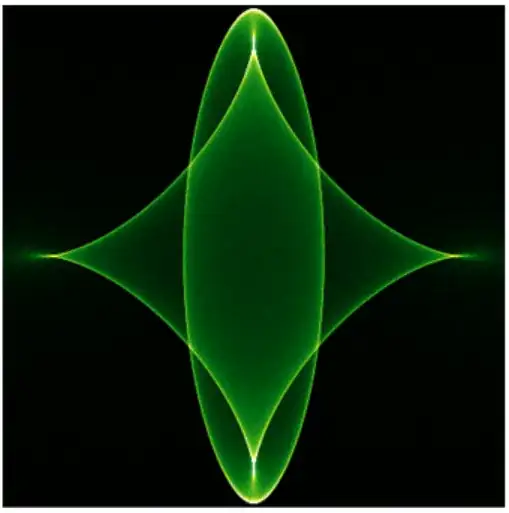
My method to extract the star-shape is to define a BoundaryMeshRegion that I can pass to Plot3D. In order to do this, I first create a color-coded root-map of the region: LightGreen: One real root, DarkGreen: Three real roots, Brown: Five real roots. As you can see in the plot, this gives an easy way to delimit the region: Simply go through the array and pick out where the lightgreen changes to darkgreen. This will then give the boundary of the star-shape.
mySumFun[s_?NumericQ, t_?NumericQ] := Module[{mySol},
mySol = {x, y} /.
NSolve[{1/5 x (-3 + 2 x^2 + 4 y^2) == s,
1/5 y (-11 + 4 x^2 + 8 y^2) == t}, {x, y}];
Plus @@ ((1/Abs[theF[#]]) & /@ mySol)
];
myCountFun[{s_?NumericQ, t_?NumericQ}] := Module[{mySol},
mySol = {x, y} /.
NSolve[{1/5 x (-3 + 2 x^2 + 4 y^2) == s,
1/5 y (-11 + 4 x^2 + 8 y^2) == t}, {x, y}];
{{s, t}, Count[mySol, {x_, y_} /; Element[x, Reals]]}
];
matrixSize = 100;
xMin = -1.;
xMax = 1.;
yMin = -1.;
yMax = 1.;
plotRange6 = {{xMin, xMax}, {yMin, yMax}};
pointData =
Array[{#2, #1} &, {matrixSize,
matrixSize}, {{yMin, yMax}, {xMin, xMax}}];
myTable = Table[
myCountFun[pointData[[i, j]]],
{i, 1, matrixSize}, {j, 1, matrixSize}];
points1 = {};
i = 0;
While[i < matrixSize,
i++;
loc = FirstPosition[myTable[[i]], {{_, _}, 3}] // First;
If[loc != "NotFound",
AppendTo[points1, myTable[[i, loc, 1]]];
];
];
points2 = {};
i = 0;
While[i < matrixSize,
i++;
loc = FirstPosition[myTable[[i]], {{_, _}, 3}] // First;
If[loc != "NotFound",
thePoint = {-myTable[[i, loc, 1, 1]], myTable[[i, loc, 1, 2]]};
AppendTo[points2, thePoint];
];
];
comboPoints = Join[points1, Reverse@points2];
regionRange = Range[Length@comboPoints];
myBoundary =
BoundaryMeshRegion[comboPoints, Line@(AppendTo[regionRange, 1])];
colorDataRules = {1 -> RGBColor[
0.7725490196078432, 0.8509803921568627, 0.7333333333333333],
2 -> RGBColor[
0.8117647058823529, 0.22745098039215686`, 0.8549019607843137],
3 -> RGBColor[
0.3764705882352941, 0.6313725490196078, 0.5843137254901961],
4 -> RGBColor[
0.7294117647058823, 0.7137254901960784, 0.7058823529411764],
5 -> RGBColor[
0.8431372549019608, 0.5882352941176471, 0.3411764705882353]}
starRootMap =
ArrayPlot[myTable[[All, All, 2]], ColorRules -> colorDataRules,
FrameTicks -> Automatic, DataRange -> plotRange6, ImageSize -> 800,
Axes -> True, AxesStyle -> White, PlotLabel -> Style["Root Map", 16]]
comboPoints = Join[points1, Reverse@points2];
regionRange = Range[Length@comboPoints];
myBoundary =
BoundaryMeshRegion[comboPoints, Line@(AppendTo[regionRange, 1])];
boundaryMesh =
Show[myBoundary, Axes -> True,
PlotLabel -> Style["BoundaryMeshRegion", 16]]

I next shade the star with a chrome color with Specularity of 1 and place it in a black background with a few extra far-distant stars:
myColor = RGBColor[0.6667, 0.6627, 0.6784]
p1C = Plot3D[mySumFun[s, t], {s, -1, 1}, {t, -1, 1},
PlotRange -> {{-1, 1}, {-1, 1}, {0, 9}}, ClippingStyle -> None,
BoxRatios -> {1, 1, 1},
RegionFunction ->
Function[{s, t}, RegionMember[myBoundary, {s, t}]],
PlotStyle -> {myColor, Specularity[White, 1]}, Mesh -> None,
Background -> Black, Boxed -> False, Axes -> None
]
backGroundStars =
Table[Graphics3D@{Specularity[White, 5], myColor,
Sphere[{RandomReal[{-5, 5}], RandomReal[{-5, 5}],
RandomReal[{10, 15}]}, RandomReal[{0.001, 0.02}]]}
, {250}];
Show[{p1C, backGroundStars}, PlotRange -> {{-5, 5}, {-5, 5}, {0, 20}}]

Update 2:
Note: I too realize this is not what the OP desired but still I learned a lot working on this. As my final version, I learned I could compose my star with another picture, preferably the dunes of Bethlehem. So that I next found a stock picture and composed my star of what I thought would be an idealized version for the three wise men to follow using the following code:
ImageCompose[image1, star, {920, 300}]
Note I can offset the star anywhere on the background with the third parameter so did so in the direction of the sunrise:



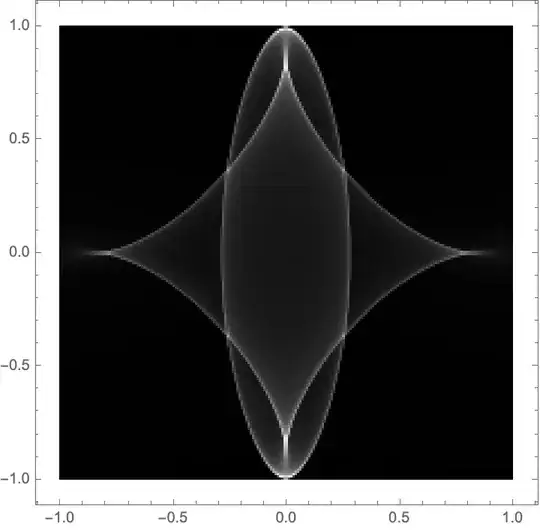












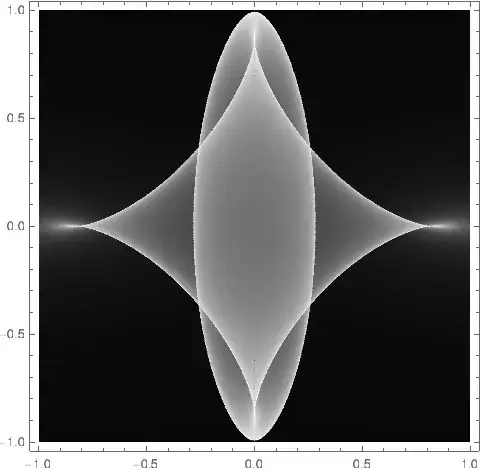
















fin Addendum? Still $[-1,1]^2$? – xzczd Dec 17 '20 at 02:55