I do not think the problem is stiffness; nor is it, arguably, scaling. The values of the solution are on the order of 10^-14 to 10^-8. The default setting for AccuracyGoal is around 8, which means that steps with an error of 10^-8 or less are acceptable. And they shouldn't be accepted with solutions that are so small.
[If you are unsure how precision and accuracy goals work in Mathematica, please see the appendix below first.]
A setting AccuracyGoal -> ag needs to be high enough so that
$$\|{\bf X(t)}\| <\mskip-4mu< 10^{-ag}$$
I would suggest setting AccuracyGoal to be about 8 digits above -Log10[size], where size is the smallest value that should be considered significantly different from zero. (One might set it to Infinity, even.)
The above rule of thumb suggests
AccuracyGoal -> 22
based on the initial condition y[0] == 1*10^(-14). In fact setting it to 16 (based on the norm of the initial conditions being approximately $\scriptstyle 10^{-8}$) or Infinity both work, too.
s = NDSolve[{x'[t] == -k1*x[t]*y[t], y'[t] == -k3*y[t] + k1*x[t]*y[t],
x[0] == 1*10^(-8), y[0] == 1*10^(-14)}, {x, y}, {t, 0, 0.001},
AccuracyGoal -> 22
];

Why do scaling and increasing WorkingPrecision work?
In @Goofy's answer, the rescaled x[t] and y[t] have values on the order of 10 to nearly 100000. So the default AccuracyGoal of around 8 is sufficiently high. One might say that the problem is poorly scaled with respect
to the accuracy goal.
Using WorkingPrecision -> 20 seems to be barely sufficient. It raises AccuracyGoal to 10. It raises PrecisionGoal to 10, too, but with a solution whose norm is around 10^-8 or less, such a PrecisionGoal should be negligible compared to the effect of AccuracyGoal. One can check that through most of integration interval, WorkingPrecision -> 20 produces a solution that has 1 to 3 digits of precision, which is in line with an error of 10^-10 in a solution of norm 10^-8. (This was estimated by comparing it with a solution computed with WorkingPrecision -> 40 and assuming this solution was highly accurate.)
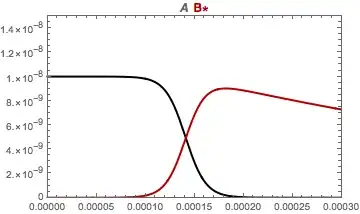
FWIW, the AccuracyGoal -> 22 solution above has 6-8 digits of precision throughout most of the integration interval. The worst precision in all methods (except the OP's) is around where the x and y components cross near t == 0.00014.
Appendix: Error norms in Mathematica.
The above discussion assumes the reader is familiar with how error is compared with PrecisionGoal -> pg and AccuracyGoal -> ag. NDSolve uses NDSolve`ScaledVectorNorm, which is discussed in Norms in NDSolve. The approach is also discussed in the documentation for PrecisionGoal and AccuracyGoal. I give a brief explanation.
Let $\bf E$ be the estimated error in the solution ${\bf X}$. If the error $\bf E$ is less than $10^{-ag} + 10^{-pg}\,\|{\bf X}\|$, then the result is accepted; if not, then in NDSolve the step size is adjusted or a warning or error is generated if the step size cannot be adjusted.
When $10^{-ag} >\mskip-4mu> 10^{-pg}\,\|{\bf X}\|$,
$$10^{-ag} + 10^{-pg}\,\|{\bf X}\| \approx 10^{-ag}$$
implies that if the error indicates that ${\bf X}$ is correct to at least $ag$ digits past the decimal point, the step is accepted.
When $10^{-pg}\,\|{\bf X}\| >\mskip-4mu> 10^{-ag}$,
$$10^{-ag} + 10^{-pg}\,\|{\bf X}\| \approx 10^{-pg}\,\|{\bf X}\|$$
implies that if the error indicates that ${\bf X}$ is correct to at least the leading $pg$ digits, the step is accepted.
Thus when
$$10^{-ag} >\mskip-4mu> 10^{-pg}\,\|{\bf X}\|$$
which usually happens when $\bf X$ is small, the errors that are nearly equal to $10^{-ag}$ are acceptable. Hence, solution values of this magnitude or less are being treated as roughly equivalent to zero. This is the issue in the OP.