Periodic von Neumann neighbours

Question

From Carl Woll's answer here, I have this code for pulling the von Neumann neighbors:

vNN[mat_, pts_] := 
  Nearest[Tuples@Range@Dimensions@mat ->Flatten@mat][pts, {All, 1}][[2 ;;]]

How do I make it so that this function wraps around (i.e, that it always pulls four values)?

Thanks

There are two good approaches in Extract four (von Neumann) neighbors of a matrix entry. What exactly doesn’t work for you in the code presented there? It seems that what you are asking would be a relatively small modification of that code. What have you tried, and what issue are you facing, so we can point you in the right direction? Otherwise your question is actually likely to be closed as a duplicate of one of those. — MarcoB, Feb 06 '21 at 13:19
Hi, thanks for the comment. On closer inspection, I agree with you. I have found that vNN[mat_, pts_] := Nearest[Tuples@Range@Dimensions@mat -> Flatten[mat]][ pts, {All, 1}][[2 ;;]] from another question suits my needs. I don't know how to wrap around so that I always have 4 values showing though, so any advice on this before this gets closed would be appreciated. Thanks — TubularHell, Feb 06 '21 at 13:21
I edited your post to emphasize that you are asking about the same for periodic boundaries. Note that you have to give credit when you take code from other users' answers. — C. E., Feb 06 '21 at 13:33
@TubularHell you could use ArrayPad[m, {1,1},"Periodic"] to generate a version of your array with wraparound padding, then extract the neighbors in that matrix. Remember to adjust the indices inside your function. — MarcoB, Feb 06 '21 at 13:40

kglr · Answer 1 · 2021-02-06T17:42:49.237

ClearAll[vNNPos, vNNVals]
vNNPos[mat_, pos_] := Transpose[Mod[pos + {{1, 0, -1, 0}, {0, 1, 0, -1}}, 
   Dimensions @ mat, 1]]

vNNVals[mat_, pos_] := Extract[vNNPos[mat, pos]] @ mat

Examples:

mat1 = {{3, 6, 9}, {12, 15, 18}, {21, 24, 27}};
mat2 = {{4, 8, 12, 16}, {20, 24, 28, 32}, {36, 40, 44, 48}, {52, 56,  60, 64}};
vNNVals[#, {2, 2}] & /@ {mat1, mat2}

 {{24, 18, 6, 12}, {40, 28, 8, 20}}

MatrixForm[MapAt[Highlighted[#, Background -> Red] &, 
     MapAt[Highlighted, #, {2, 2}], vNNPos[#, {2, 2}]]] & /@ 
   {mat1, mat2} // Row[#, Spacer[10]] &

vNNVals[#, {2, 1}] & /@ {mat1, mat2}

 {{21, 15, 3, 18}, {36, 24, 4, 32}}

MatrixForm[MapAt[Highlighted[#, Background -> Red] &, 
     MapAt[Highlighted, #, {2, 1}], vNNPos[#, {2, 1}]]] & /@ 
  {mat1, mat2} // Row[#, Spacer[10]] &

A little mouse on the pampas · Answer 2 · 2021-02-07T03:08:55.807

I wrote the following code using the method of finding where the horse can go in the chess board:

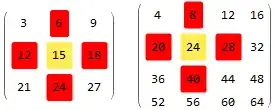
matrix = {{3, 6, 9}, {12, 15, 18}, {21, 24, 
   27}};
value = 15;(*The value of the central element*)
{m, n} = Dimensions[matrix];
Board = Table[0, {m + 1}, {n + 1}];
Moves0 = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}};
Moves = Nest[
   DeleteDuplicates[Flatten[Outer[Plus, #, Moves0, 1], 1]] &, {{0, 
     0}}, 1(*step number*)];
InRangeAndEmpty[{x_, y_}] := (1 <= x <= m && 1 <= y <= n && 
    Board[[x, y]] == 0);
Accessibility[{x_, y_}] := 
  Module[{accessibility = 0, a = 1}, 
   While[a <= 8, 
    If[InRangeAndEmpty[{x + Moves[[a, 1]], y + Moves[[a, 2]]}], 
     accessibility++]; a++];
   accessibility];
GetNextMove[{x_, y_}] := 
  MapIndexed[{First[#2], #1} &, 
   SortBy[Select[
     Table[{x + Moves[[i, 1]], y + Moves[[i, 2]]}, {i, 
       Length[Moves]}], InRangeAndEmpty], 
    N@Arg[#[[2]] - x + (#[[1]] - y) I] &]];
matrix[[#1, #2]] & @@@ (GetNextMove[
    Position[matrix, value] // First][[All, 2]])
MatrixForm[
   MapAt[Highlighted[#, Background -> Red] &, 
    MapAt[Highlighted, #, First[Position[matrix, value]]], 
    GetNextMove[
      Position[#, value(The value of the central element)] // 
       First][[All, 2]]]] &@matrix

If you need periodic filling, you only need to increase some feasible ways of moves:

Moves0 = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}, {m - 1, 0}, {-(m - 1), 
    0}, {0, -(n - 1)}, {0, n - 1}};

Moves0 = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}, {m - 1, 0}, {-(m - 1), 
    0}, {0, -(n - 1)}, {0, n - 1}};
matrix = {{4, 8, 12, 16}, {20, 24, 28, 32}, {36, 40, 44, 48}, {52, 56,
     60, 64}};
position = {1, 1};(*The position of the central element*)
{m, n} = Dimensions[matrix];
Board = Table[0, {m + 1}, {n + 1}];
Moves0 = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}, {m - 1, 0}, {-(m - 1), 
    0}, {0, -(n - 1)}, {0, n - 1}};
Moves = Nest[
   DeleteDuplicates[Flatten[Outer[Plus, #, Moves0, 1], 1]] &, {{0, 
     0}}, 1(*step number*)];
InRangeAndEmpty[{x_, y_}] := (1 <= x <= m && 1 <= y <= n && 
    Board[[x, y]] == 0);
Accessibility[{x_, y_}] := 
  Module[{accessibility = 0, a = 1}, 
   While[a <= 8, 
    If[InRangeAndEmpty[{x + Moves[[a, 1]], y + Moves[[a, 2]]}], 
     accessibility++]; a++];
   accessibility];
GetNextMove[{x_, y_}] := 
  MapIndexed[{First[#2], #1} &, 
   SortBy[Select[
     Table[{x + Moves[[i, 1]], y + Moves[[i, 2]]}, {i, 
       Length[Moves]}], InRangeAndEmpty], 
    N@Arg[#[[2]] - x + (#[[1]] - y) I] &]];
matrix[[#1, #2]] & @@@ (GetNextMove[position][[All, 2]])
MatrixForm[
   MapAt[Highlighted[#, Background -> Red] &, 
    MapAt[Highlighted, #, 
     position(The position of the central element)], 
    GetNextMove[position][[All, 2]]]] &@matrix

Reference link:趣味象棋一马平川 https://demonstrations.wolfram.com/TheKnightsTour/

score 4 · Answer 3 · answered Feb 07 '21 at 03:42

Adapting my answer to Imposing a Periodic Boundary Condition in Nearest Neighbour Search:

dist[a_, b_, d0_] := Norm@Mod[a - b, d0, -d0/2];
vNN[mat_, pts_] := Rest@Nearest[
     Tuples@Range@Dimensions@mat -> Flatten@mat, 
     pts, {All, 1 + $MachineEpsilon},
     DistanceFunction -> (dist[##, Dimensions@mat] &)];

Example:

mat = Table[10 i + j, {i, 4}, {j, 6}];
mat // MatrixForm
vNN[mat, {2, 2}]
vNN[mat, {1, 1}]
vNN[mat, {4, 5}]

For some reason the radius 1 needs to be replaced with something slightly greater, for instance 1 + $MachineEpsilon.

Periodic von Neumann neighbours

3 Answers3