1

I want to expand a two-variable function up to asymmetric orders in two expansion variables, i.e.

$$f(x,y) = T[f(x,y)] + \mathcal{O}(x^2,y^3,xy,xy^2).$$

Note that, while quadratic terms in $y$ are retained, the (also!) quadratic terms in $xy$ are contained in the higher-order terms. Hence the asymmetry (and the ultimate origin of the problem).

The intuitive two-variable expansion

Series[f[x,y],{x,x0,1},{y,y0,2}]

includes some of the undesired terms, namely $xy$ and $xy^2$.

I've seen the (maybe) related post Multivariable Taylor expansion does not work as expected. However, in this post the issue with the asymmetry in the two expansion variables is not commented, so the answers there are not directly applicable (in the best case).

Is there a simple way/function to perform this calculation?

Pablo G
  • 13
  • 3
  • 2
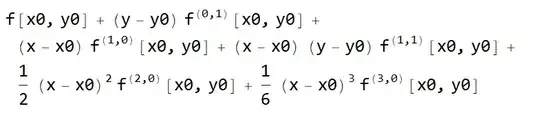
    Function f[x,y]==-f[-x,y] is asymmetric in x? – Ulrich Neumann Mar 04 '21 at 10:56
  • Perhaps your question finds an answer if you tell us something about the relationship O[x-x0]=?=O[(y-y0)^alfa] , alfa=2/3 or 3/2? or ...? – Ulrich Neumann Mar 04 '21 at 11:16
  • In my problem there is no simple transformation rule for the function f[x,y] like the one you are metioning in your comment.

    With respect to the orders of magnitude, you have approximately $\mathcal{O}(x) = \mathcal{O}(y^2)$, if that helps.

     – Pablo G Mar 04 '21 at 11:36
  • Why not compute all terms and then replace the unwanted terms by zero? – Daniel Huber Mar 04 '21 at 13:43
  • Could modify the method in the related posts by weighting. I show this for the case of expansion at the origin. `In[28]:= Normal[ Series[f[x, y] /. {x -> t^3x, y -> t^2y}, {t, 0, 4}]] /. t -> 1

    Out[28]= f[0, 0] + yDerivative[0, 1][f][0, 0] + (1/2)y^2Derivative[0, 2][f][0, 0] + xDerivative[1, 0][f][0, 0]`

     – Daniel Lichtblau Mar 04 '21 at 15:14
  • I should read responses more often. What I did is substantially similar to the method given by @UlrichNeumann – Daniel Lichtblau Mar 04 '21 at 15:15

1 Answers1

4

If you know that O[x-x0]==O[(y-y0)^2] the taylor expansion follows to

Normal[Series[f[x, y] /. {x -> x0 + eps (x - x0),y -> y0 + eps^2 (y - y0)}, {eps, 0, 3}]] /. eps -> 1

enter image description here

Ulrich Neumann
  • 53,729
  • 2
  • 23
  • 55