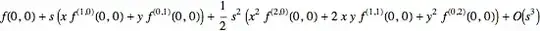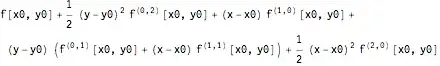77

The basic multivariable Taylor expansion formula around a point is as follows:

$$ f(\mathbf r + \mathbf a) = f(\mathbf r) + (\mathbf a \cdot \nabla )f(\mathbf r) + \frac{1}{2!}(\mathbf a \cdot \nabla)^2 f(\mathbf r) + \cdots \tag{1}$$

In Mathematica, as far as I know, there is only one function, Series that deals with Taylor expansion. And this function surprisingly doesn't expand functions in the way the above multivariable Taylor expansion formula does. What I mean is that the function Series doesn't produce a Taylor series truncated at the right order.

For example, if I want to expand $f(x,y)$ around $(0,0)$ to order $2$, I think I should evaluate the following Mathematica expression:

Normal[Series[f[x,y],{x,0,2},{y,0,2}]]

But the result also gives order $3$ and order $4$ terms. Of course, I can write the expression in the following way to get a series truncated at order $2$: 

Normal[Series[f[x,y],{x,0,1},{y,0,1}]]

but in this way I lose terms like $x^2$ and $y^2$, so it is still not right.

The formula $(1)$ gives each order in each term, so if the function Series would expand a function in the way formula $(1)$ does, there will be no problem.

I am disappointed that the Mathematica developers designed Series as they did. Does anyone know how to work around this problem?

J. M.'s missing motivation
  • 124,525
  • 11
  • 401
  • 574
matheorem
  • 17,132
  • 8
  • 45
  • 115
  • TLDR version: The OP does not have a problem with Series in Mathematica but with a Taylor series is to begin with. Series is giving the expected Taylor series. What the OP wants is a Taylor series in two variables under the additional assumption x~y. This additional assumption can easily be implemented by substituting x=tX and y=tY and taking a series in t instead. Note that it is a good thing that Series in Mathematica does not work like this by default because very often this would not be desired and would be very unexpected behavior for a multivariate Taylor series. – Kvothe Aug 10 '21 at 16:06
  • 1
    Discussion on wolfram community -- https://community.wolfram.com/groups/-/m/t/2353053?p_p_auth=8FpuUkxs – Yaroslav Bulatov Aug 30 '21 at 07:42

5 Answers5

87

It's true that the multivariable version of Series can't be used for your purpose, but it's still pretty straightforward to get the desired order by introducing a dummy variable t as follows:

Normal[Series[f[(x - x0) t + x0, (y - y0) t + y0], {t, 0, 2}]] /. t -> 1

$(x-\text{x0}) (y-\text{y0}) f^{(1,1)}(\text{x0},\text{y0})+\frac{1}{2} (x-\text{x0})^2 f^{(2,0)}(\text{x0},\text{y0})+(x-\text{x0}) f^{(1,0)}(\text{x0},\text{y0})+(y-\text{y0}) f^{(0,1)}(\text{x0},\text{y0})+\frac{1}{2} (y-\text{y0})^2 f^{(0,2)}(\text{x0},\text{y0})+f(\text{x0},\text{y 0})$

The expansion is done only with respect to t which is then set to 1 at the end. This guarantees that you'll get exactly the terms up to the total order (2 in this example) that you specify.

Jens
  • 97,245
  • 7
  • 213
  • 499
32

Here's an attempt:

multiTaylor[f_, {vars_?VectorQ, pt_?VectorQ, n_Integer?NonNegative}] :=
                   Sum[Nest[(vars - pt).# &, (D[f, {vars, \[FormalK]}]
                       /. Thread[vars -> pt]), \[FormalK]]/\[FormalK]!,
                       {\[FormalK], 0, n}, Method -> "Procedural"]

multiTaylor[f[x, y], {{x, y}, {0, 0}, 2}]
   f[0, 0] + y*Derivative[0, 1][f][0, 0] + x*Derivative[1, 0][f][0, 0] +
   (y*(y*Derivative[0, 2][f][0, 0] + x*Derivative[1, 1][f][0, 0]) +
    x*(y*Derivative[1, 1][f][0, 0] + x*Derivative[2, 0][f][0, 0]))/2
J. M.'s missing motivation
  • 124,525
  • 11
  • 401
  • 574
  • I admire your mathematica skill. Your answer is right. But I think the following Jens's solution is better, it is simple and more enlightening. What do you think? Thank you all the same!! – matheorem Nov 22 '12 at 08:21
  • 1
    No problem; you should always pick the answer that is most helpful to you and give that answer the acceptance, after all. I wanted to write something a bit more general (i.e. something that can also handle three, four... variables), so mine is a little bit complicated. – J. M.'s missing motivation Nov 22 '12 at 08:24
  • Thanks for the function – it's very useful to me. One slight problem I just noticed occurs when f contains the variable k, which will be replaced by some integer after the expansion. To improve you function, you might want to wrap it in Module[{k}, (* function code *)] to protect the local variable. – David Zwicker Jul 30 '15 at 20:07
  • @David, you're right; I'll incorporate the fix later. Thank you! – J. M.'s missing motivation Jul 30 '15 at 22:02
  • 1
    This function should be implemented in Mathematica – Capivara Cometa Sep 09 '19 at 20:16
22

Jens answered this nicely. But my preferred way of thinking about this question is via re-scaling (essentially using perturbation theory) instead of dummy variables.

For example, to generate the series expansion, re-scale all variables by s and expand by series coercion: 

(f[x,y] /. Thread[{x,y} -> s {x,y}]) + O[s]^3

TraditionalForm output

This form is generally useful—and although one can use Normal, often working with the series is what you really end up wanting to do.

TheDoctor
  • 2,832
  • 1
  • 14
  • 17
  • Thank you so much! O[s] is doing like magic. I am wondering how O is defined, it behaves not like a normal function. – matheorem Apr 16 '18 at 00:36
  • Not magic. If you add a function to a series expansion, the only way for it to make sense is to automatically coerce the function into a series (about the same expansion point). – TheDoctor Apr 22 '18 at 06:04
  • If you add 1.0 to Pi, what you would expect should happen. You might consider this to be "magic" too but surely such automatic coercion is what you want to happen... – TheDoctor Apr 22 '18 at 06:16
  • Finally, I should have pointed out that Series automatically generates O. For example, if you enter Series[f[x],{x,0,3}] then you'll see O[x] in the output. – TheDoctor Apr 22 '18 at 06:18
10

Another possibility is to strip the "too high" terms with a rule:

ser = Series[f[x, y], {x, x0, 2}, {y, y0, 2}];
Normal[ser] /.
 Derivative[m__][f][args__] /; Plus[m] > 2 :> 0

Mathematica graphics

Peter Breitfeld
  • 5,182
  • 1
  • 24
  • 32
2

If f is dependent on a variable k, the above definition leads to a conflict. It is better to rename k in a less common name such as var.

multiTaylor[f_, {vars_?VectorQ, pt_?VectorQ, n_Integer?NonNegative}] :=
                   Sum[Nest[(vars - pt).# &, (D[f, {vars, var}] /. Thread[vars -> pt]),var]/var!,
                       {var, 0, n}, Method -> "Procedural"]
Drakonomikon
  • 191
  • 7