Marking a Continuous Plot With The Same Subinterval Based on The Range of The Codomain

Question

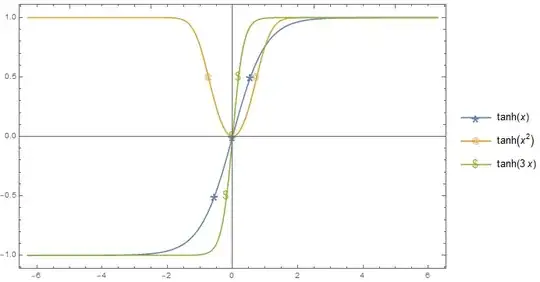
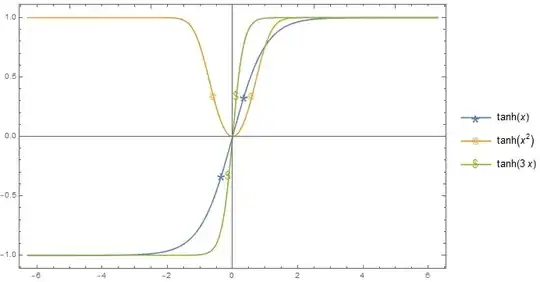
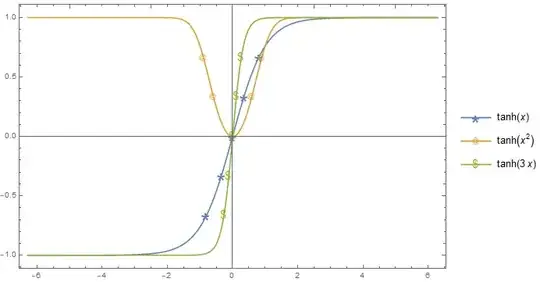
Consider the following plot

n := 1
f[x_] := {Tanh[x], Tanh[x^2], Tanh[3 x]};
DiscretePlot[Evaluate[f[x]], {x, -2 Pi, 2 Pi, n}, PlotRange -> All, 
 Filling -> None, PlotMarkers -> {{"*", 25}, {"@", 10}, {"$", 15}}, 
 PlotLegends -> "Expressions", Frame -> True, Joined -> True]

I want two changes.

1. Joined -> True is replaced by continuous curve (the plot should be smooth).
2. Since the Codomain is $y\in(-1,1)$, i need to divide the interval into n-subdivision based on the codomain (not the domain). So, for example if $n=2$, there will be three marks that divide the range of the codomain into $3$ equal parts.

Here is the illustration that might help to understand, this illustration below isn't the same as the original plot for simplification purpose:

Notice there are ($=$) symbols to indicate that the range of the codomain is divided into n-equal parts correspond to the marks of the graph.

My attempt is combining plot and discrete plot with show, but still have no idea about dividing the range of the codomain.

n := 20
f[x_] := {Tanh[x], Tanh[x^2], Tanh[3 x]};
Show[DiscretePlot[Evaluate[f[x]], {x, -2 Pi, 2 Pi, n}, 
  PlotRange -> All, Filling -> None, 
  PlotMarkers -> {{"*", 25}, {"@", 10}, {"$", 15}}, 
  PlotLegends -> "Expressions", Frame -> True], 
 Plot[{Tanh[x], Tanh[x^2], Tanh[3 x]}, {x, -2 Pi, 2 Pi}]]

Reference:

1. Plot with plot markers without using ListPlot
2. https://community.wolfram.com/groups/-/m/t/108265

Answer 1

We can use Plot with the options MeshFunctions -> {#2 &} and Mesh -> n to mark n points on the curves:

f[x_] := {Tanh[x], Tanh[x^2], Tanh[3 x]};
markers = {{"*", 25}, {"@", 10}, {"$", 15}};
mesh = 3;
plot = Plot[Evaluate[f[x]], {x, -2 Pi, 2 Pi}, PlotRange -> All, 
  Filling -> None, 
  PlotLegends -> LineLegend["Expressions", LegendMarkers -> markers, 
    LegendMarkerSize -> {40, 20}], 
  Frame -> True, 
  MeshFunctions -> {#2 &}, 
  Mesh -> mesh, 
  MeshStyle -> PointSize[Large], 
  ImageSize -> Large]

Post-process to replace points with appropriate markers:

meshStyles = Association[Join @@ 
   Cases[plot, 
     {___, Directive[___, c_?ColorQ, ___], Line[x_]} :> Thread[x -> c],
     All]];
styleToMarkers = AssociationThread[ColorData[97] /@ Range[3], Style @@@ markers];
plot /. Point[x_] :> ({meshStyles@#, Text[styleToMarkers[meshStyles@#], #]} & /@ x)

Replace mesh = 3 above with mesh = {Most @ Subdivide[-1, 1, 3]} to get

Use Mesh -> 2 to get

Use mesh = 5 to get