Marking with Mesh, Distinct coloring, Ticksing, and Plotting table of complex function with parametric plot

Question

Here is my todo list and what i've done:

1. Using FrameTicks on specific points only (failed).
2. Plotting six graphs with Table on ParametricPlot (Success).
3. Marking each graph with Mesh "independently" (have no idea, but have the related topic, See 8).
4. Coloring each graph (failed).
5. Legending each graph (works but only the first graph).

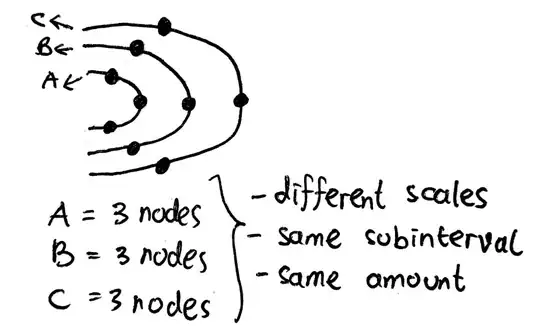
I will explain the point $(3)$ with this sketch (simplification drawing):

The distance between two marks based on the codomain should have the same length.

Here is my attempt without different marks:

M = 5;
markers = {{"*", 25}, {"@", 10}, {"$", 15}, {"#", 10}, {"&", 
    10}, {"+", 25}};
mesh = {Most@Subdivide[-2, 2.8, 5]};
eqn = Table[
   2 M/t (\[Theta] Cot[\[Theta]] + I  \[Theta]), {t, {9, 19, 24, 29, 
     39, 49}}];
ticks = {{{-5, -2}, -4, -3, -2, -1, 0, 1}, {-Pi, Pi}, {}, {}};
graph = ParametricPlot[ReIm@eqn, {\[Theta], -3.14, 3.14}, 
  AspectRatio -> 1, 
  FrameLabel -> {"Re(s(\[Theta]))", "Im(s(\[Theta]))"}, 
  Frame -> True, FrameTicks -> ticks, PlotStyle -> Thick, 
  Axes -> False, MeshFunctions -> {#2 &}, Mesh -> mesh, 
  MeshStyle -> PointSize[Large], 
  PlotLegends -> 
   Placed[LineLegend[{"t=9", "t=19", "t=24", "t=29", "t=39", "t=49"}, 
     LegendFunction -> "Frame"], {.85, .8}]]

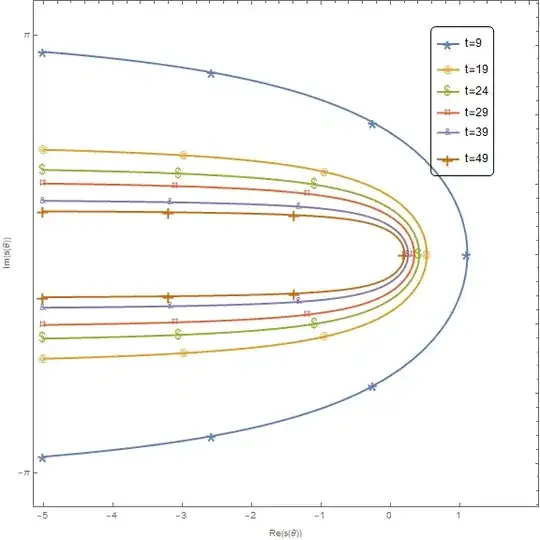
The Output:

The markings still sharing the same scale and not evaluated on each graph, has no coloring, FrameTicks doesn't work, and the Legend only shows $1$ graph.

Meanwhile, when i try to add the different markings, it becomes messy and there's an error message

M = 5;
markers = {{"*", 25}, {"@", 10}, {"$", 15}, {"#", 10}, {"&", 
    10}, {"+", 25}};
mesh = {Most@Subdivide[-2, 2.8, 5]};
eqn = Table[
   2 M/t (\[Theta] Cot[\[Theta]] + I  \[Theta]), {t, {9, 19, 24, 29, 
     39, 49}}];
ticks = {{{-5, -2}, -4, -3, -2, -1, 0, 1}, {-Pi, Pi}, {}, {}};
graph = ParametricPlot[ReIm@eqn, {\[Theta], -3.14, 3.14}, 
   AspectRatio -> 1, 
   FrameLabel -> {"Re(s(\[Theta]))", "Im(s(\[Theta]))"}, 
   Frame -> True, FrameTicks -> ticks, PlotStyle -> Thick, 
   Axes -> False, MeshFunctions -> {#2 &}, Mesh -> mesh, 
   MeshStyle -> PointSize[Large], 
   PlotLegends -> 
    Placed[LineLegend[{"t=9", "t=19", "t=24", "t=29", "t=39", "t=49"},
       LegendFunction -> "Frame"], {.85, .8}]];
meshStyles = 
  Association[
   Join @@ Cases[
     graph, {___, Directive[___, c_?ColorQ, ___], Line[x_]} :> 
      Thread[x -> c], All]];
styleToMarkers = 
  AssociationThread[ColorData[97] /@ Range[3], Style @@@ markers];
graph /. Point[
   x_] :> ({meshStyles@#, Text[styleToMarkers[meshStyles@#], #]} & /@ 
    x)

Output:

And i wish i have something like this:

Hope my question isn't too much and you want to help me. Thanks in advance!

Here is my references:

1. parametricplot-table-of-complex-functions-in-several-graphs
2. coloring-parametricplot-of-several-complex-functions
3. color-parametric-plot-by-parameter
4. marking-a-continuous-plot-with-the-same-subinterval-based-on-the-range-of-the-co
5. how-do-i-reverse-the-axis-in-parametricplot

Answer 1

1. Wrap the first argument of ParametricPlot with Evaluate to get the 6 curves treated as separate curves so that each has its own style end legend entry.

2. Add LegendMarkers -> markers in LineLegend[...]

3. Replace 3 in the definition of styleToMarkers with Length @ markers.

4. Define ticks as ticks = {{{-Pi, Pi}, Automatic}, {Range[-5, 1], Automatic}};

5. Add the option Exclusions -> None: This makes each curve a single line rather than two lines, and ensures that meshStyles works without modification.

6. Use the options MeshFunctions -> {"ArcLength"} and Mesh -> 5 to add 5 markers that divide each curve into 6 equal-length pieces.

7. Add the option RegionFunction -> (-5 <= # <= 2 &): This ensures that the underlying curves produced by the kernel do not extend to the left of -5. (PlotRange does not guarantee this.) Without this option, MeshFunctions -> {"ArcLength"} will not give the desired result.

With all these changes:

graph = ParametricPlot[Evaluate[ReIm@eqn], {θ, -3.14, 3.14},
   PlotStyle -> Thick, AspectRatio -> 1, 
   FrameLabel -> {"Re(s(θ))", "Im(s(θ))"},
   Frame -> True, FrameTicks -> ticks, Axes -> False, 
   ImageSize -> Large,
   MeshStyle -> PointSize[Large],
   MeshFunctions -> {"ArcLength"},
   Mesh -> 5,
   Exclusions -> None,
   RegionFunction -> (-5 <= # <= 2 &),
   PlotRange -> {{-5, 2}, Automatic},
   PlotRangePadding -> Scaled[.02],
   PlotLegends -> Placed[LineLegend[{"t=9", "t=19", "t=24", "t=29", "t=39", "t=49"},
       LegendFunction -> "Frame", LegendMarkers -> markers], {.85, .8}]];
meshStyles = Association[Join @@ Cases[graph, 
   {___, Directive[___, c_?ColorQ, ___], Line[x_]} :> Thread[x -> c], All]];
styleToMarkers = AssociationThread[ColorData[97] /@ Range[Length @ markers], 
   Style @@@ markers];
ticks = {{{-Pi, Pi}, Automatic}, {Range[-5, 1], Automatic}};
graph /. Point[x_] :> ({meshStyles@#, Text[styleToMarkers[meshStyles@#], #]} & /@ x)

To add markers at the start and end of curves use

graph /. {Point[x_] :> ({meshStyles@#, Text[styleToMarkers[meshStyles@#], #]} & /@ x), 
 Line[x_] :> {Line[x], 
    {meshStyles@#, Text[styleToMarkers[meshStyles@#], #]} & /@ x[[{1, -1}]]}}