4

Given the quadratic form

f[x_,y_,z_]:=200.456+2.340*10^10*x^2+7.99*10^7*y^2+
  y*(2.80*10^(-9)-1.1735*10^6*z) -29150.591*z+1.895*10^6*z^2+
  x(-4.329*10^6-9.731*10^7*y+3.135*10^8*z);

I define the ellipsoid defined by $f(x,y,z)\leq 1$ as follows

RegionPlot3D[f[x, y, z] <= 1 ,
 {x, 0.00008, 0.000102}, {y, -0.0000555, 0.00017}, {z, -0.00099, 0.0012}, 
 AxesLabel -> {x, y, z}, Mesh -> None, ImageSize -> Medium, 
 PlotPoints -> 50]

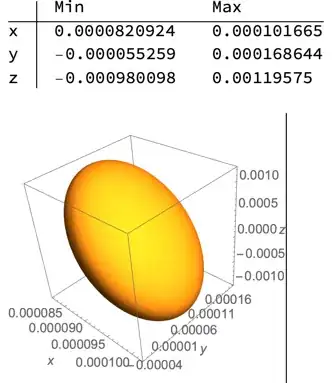
enter image description here

I would like to obtain the projection of the ellipsoid onto each one of the $Ox$, $Oy$ and $Oz$ axes.

Also, can we do the projection in the wall of the x-y, y-z, and z-x plane so that the black point is also visible into the wall?

Michael E2
  • 235,386
  • 17
  • 334
  • 747
Sahabub Jahedi
  • 461
  • 2
  • 8
  • Possible duplicate: https://mathematica.stackexchange.com/questions/199612/how-to-project-3d-image-in-the-planes-xy-xz-yz – Michael E2 Apr 13 '21 at 00:38
  • Related: https://mathematica.stackexchange.com/questions/189470/find-bounding-box-of-arbitrary-3d-graphics -- Also, possibly: https://mathematica.stackexchange.com/questions/92466/how-to-show-the-projections-of-3d-orbit-on-the-three-primary-planes – Michael E2 Apr 14 '21 at 21:51

5 Answers5

8

Using @kglr's projectToWalls:

(* https://mathematica.stackexchange.com/a/199613/4999 *)
ClearAll[projectToWalls]
projectToWalls = 
  Module[{pr = PlotRange[#]}, 
    Normal[#] /. 
     Line[x_, ___] :> {Line[x], 
       Line[x /. {a_, b_, c_} :> {pr[[1, 1]], b, c}], 
       Line[x /. {a_, b_, c_} :> {a, pr[[2, 2]], c}], 
       Line[x /. {a_, b_, c_} :> {a, b, pr[[3, 1]]}]}] &;

cp = ContourPlot3D[
  200.456 + 2.34010^10x^2 + 7.9910^7y^2 + 
    y(2.8010^(-9) - 1.173510^6z) - 29150.591z + 1.89510^6z^2 + 
    x(-4.32910^6 - 9.73110^7y + 3.13510^8*z) == 1, {x, 0.00008, 
   0.00011}, {y, -0.00011, 0.00022}, {z, -0.0015, 0.0015}];


projectToWalls@cp

enter image description here

Update:

If range of cp on axes is actually desired (since an ellipsoid is path-connected):

PlotRange@Show[cp, PlotRangePadding -> 0, PlotRange -> All]
(*
{{ 0.0000820059, 0.0001018},
 {-0.0000560249, 0.000169893},
 {-0.000991714,  0.00119972}}
*)

This is a numerical approximation. For more accuracy, increase PlotPoints or MaxRecursion. With MaxRecursion -> 4, we get the following:

{{ 0.0000819949, 0.000101789},
 {-0.000055904,  0.000169853},
 {-0.000990615,  0.00119862}}

Second update:

For more control of what is projected (requested in a comment):

ClearAll[projectToWalls]
projectToWalls[g_Graphics3D, prim_ : Line] := 
  Module[{pr = PlotRange[g]},
   Normal[g] /. (p : prim)[x_, r___] :> {p[x, r],
      p[x /. {a_?NumericQ, b_?NumericQ, c_?NumericQ} :>
         {pr[[1, 1]], b, c}],
      p[x /. {a_?NumericQ, b_?NumericQ, c_?NumericQ} :>
         {a, pr[[2, 2]], c}],
      p[x /. {a_?NumericQ, b_?NumericQ, c_?NumericQ} :>
         {a, b, pr[[3, 1]]}]}];

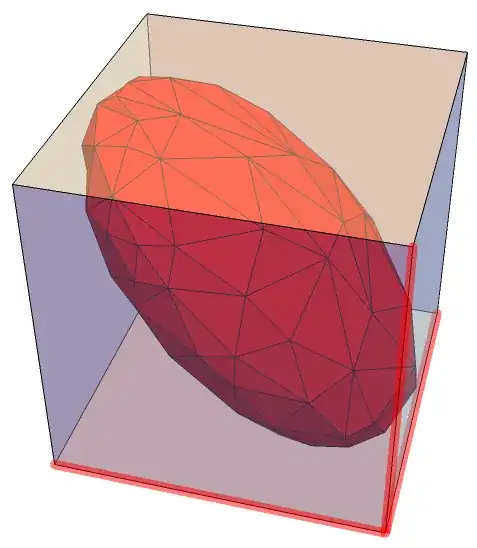
Example from comment:

cp = Show[
   ContourPlot3D[
    200.456 + 2.340*10^10*x^2 + 7.99*10^7*y^2 + 
      y*(2.80*10^(-9) - 1.1735*10^6*z) - 29150.591*z + 
      1.895*10^6*z^2 + 
      x*(-4.329*10^6 - 9.731*10^7*y + 3.135*10^8*z) == 1, {x, 0.00008,
      0.00011}, {y, -0.00011, 0.00022}, {z, -0.0015, 0.0015}, 
    ContourStyle -> Directive[{Orange, Opacity[0.5]}], Mesh -> None], 
   Graphics3D[{Black, PointSize[0.02], 
     Point[{9.19*10^(-5), 5.67*10^(-5), 10.78*10^(-5)}]}]];
projectToWalls[cp, Polygon | Point]

Notes: Point as well as geometric 3D shapes can be rendered in Graphics3D only as 3D shapes, not flat projections. To get a 2D projection would require subroutines that discretize these objects to polygons that are projected flat against the bounding box. Projecting polygons results in overlapping polygons that do not look good usually.

Michael E2
  • 235,386
  • 17
  • 334
  • 747
  • The question is about the projections on the coordinate axes, not the coordinate planes. This is not it. – user64494 Apr 13 '21 at 06:02
  • I wonder the upvotes for the incorrect answer. – user64494 Apr 13 '21 at 06:54
  • Yes. @user64494, you are absolutely right. – Sahabub Jahedi Apr 13 '21 at 07:20
  • Show[ContourPlot3D[ 200.456 + 2.34010^10x^2 + 7.9910^7y^2 + y(2.8010^(-9) - 1.173510^6z) - 29150.591z + 1.89510^6z^2 + x(-4.32910^6 - 9.73110^7y + 3.13510^8z) == 1, {x, 0.00008, 0.00011}, {y, -0.00011, 0.00022}, {z, -0.0015, 0.0015}, ContourStyle -> Directive[{Orange, Opacity[0.5]}], Mesh -> None], Graphics3D[{Black, PointSize[0.02], Point[{9.1910^(-5), 5.6710^(-5), 10.7810^(-5)}]}]]. Using this code can we do the projection in the wall of the x-y, y-z, and z-x plane so that the black point is also visible into the wall? – Sahabub Jahedi Apr 13 '21 at 14:18
  • @Michael E2 please see it. – Sahabub Jahedi Apr 13 '21 at 14:19
  • @user64494 please see it. – Sahabub Jahedi Apr 13 '21 at 14:19
  • 1
    @SahabubJahedi Why not edit your original post and add the detail of your require!!! – cvgmt Apr 13 '21 at 14:26
  • Like people have never misspoken. The question body is code-only, which does not inspire confidence that thoughtfulness underlies the post. Nonetheless, the OP first agrees with user64494 and now follows up for an extension to projecting on the walls. - This answer was intended to show the OP whether the proposed duplicate solves the problem adequately. – Michael E2 Apr 13 '21 at 14:26
  • That https://www.dropbox.com/s/bxak6w9lvg2yd2r/%D0%97%D0%BD%D1%96%D0%BC%D0%BE%D0%BA%20%D0%B5%D0%BA%D1%80%D0%B0%D0%BD%D0%B0%202021-04-13%2009.58.09.png?dl=0 was the answer by@MichaelE2 before his edit. Compare with my answer. In such cases I submit a new answer. – user64494 Apr 13 '21 at 15:13
  • 1
    For those who don't know how to use the site, you can find previous edits more easily than going to dropbox by clicking on the "edit...ago" link in the middle to the left of the name/"community wiki". But I think it's easy enough just to look at the current post, since I marked the update by posting it below "Update". The only change I made above that was changing Out[] to a variable cp, so I could reuse it in the update. Strange to be criticized by a commenter for responding to their criticism in an early comment -- it starts to resemble harassment. – Michael E2 Apr 13 '21 at 18:26
  • @MichaelE2, I have tried a lot to edit the question but I don't know why always it is showing some error. I don't understand why. – Sahabub Jahedi Apr 14 '21 at 05:30
  • @SahabubJahedi I don't know either, especially with no hint as to what the error is. I thought there was an automatic check that would reject questions that we all or mostly code. Since your original post went through, they must have gotten rid of it. There were some bugs in it. – Michael E2 Apr 14 '21 at 12:55
2

This can be done in such a way. First, we define the set under consideraration as anImplicitRegion, raionalizing it for convenience:

r = ImplicitRegion[Rationalize[
200.4 + 2.3*10^10 x^2 + 8*10^7 y^2 + 
y*(2.8*10^-9 - 1.17*10^6*z) - 29150.6*z + 1.9*10^6*z^2 + 
x*(-4.3*10^6 - 9.73*10^7*y + 3.13*10^8*z) == 1 && 
x >= 0.00008 && x <= 0.00011 && y >= -0.00011 && y <= 0.00022 && 
z >= -0.0015 && z <= 0.0015, 10^-35], {x, y, z}];

Second, we project r onto the $x$-axis by

rx = TransformedRegion[r, Function[p, {p[[1]], 0, 0 }]];

Finally,

FullSimplify[RegionMember[rx, {x, y, z}]]

y == 0 && z == 0 && 3 \[Sqrt]190042183023602016355407785916095142401 + 3066319841000000000000000 x >= 287992553863649997529 && 3066319841000000000000000 x <= 287992553863649997529 + 3 \[Sqrt]190042183023602016355407785916095142401

Addition. As the OP noticed, the ranges of the variables are not needed here. A typo in the equation of the ellipsiod is corrected too.

r1 = ImplicitRegion[Rationalize[
200.456 + 2.340*10^10*x^2 + 7.99*10^7*y^2 + 
y*(2.80*10^(-9) - 1.1735*10^6*z) - 29150.591*z + 
1.895*10^6*z^2 + 
x*(-4.329*10^6 - 9.731*10^7*y + 3.135*10^8*z) == 1, 10^-35], {x,
y, z}];
rx1 = TransformedRegion[r, Function[p, {p[[1]], 0, 0 }]];
FullSimplify[RegionMember[rx1, {x, y, z}]]

65785848361558179853764884731429 + 25000000000000 x (-57941282080071571622229 + 315245111239400000000000000 x) <= 0 && y == 0 && z == 0

Reduce[65785848361558179853764884731429 + 
25000000000000 x (-57941282080071571622229 + 
315245111239400000000000000 x) <= 0 && y == 0 && z == 0, {x, y, z}, Reals] // N

0.0000819931 <= x <= 0.000101804 && y == 0. && z == 0.

user64494
  • 26,149
  • 4
  • 27
  • 56
  • Another approach consists in Maximize[z, Rationalize[ 200.4 + 2.3*10^10 x^2 + 8*10^7 y^2 + y*(2.8*10^-9 - 1.17*10^6*z) - 29150.6*z + 1.9*10^6*z^2 + x*(-4.3*10^6 - 9.73*10^7*y + 3.13*10^8*z) == 1 && x >= 0.00008 && x <= 0.00011 && y >= -0.00011 && y <= 0.00022 && z >= -0.0015 && z <= 0.0015, 10^-35], {x, y, z}]//N which performs {0.0014372, {x -> 0.0000838291, y -> 0.0000614881, z -> 0.0014372}}. – user64494 Apr 13 '21 at 07:12
  • Thank you so much. I have given the limits i.e. {x,0.00008,0.00011},{y,-0.00011,0.00022},{z,-0.0015,0.0015} just to draw the ellipsoid. My object is to take the projections of this ellipsoid 200.456+2.34010^10x^2+7.9910^7y^2+y(2.8010^(-9)-1.173510^6z) - 29150.591z+1.89510^6z^2+x(-4.32910^6-9.73110^7y+3.13510^8*z)==1 on x,y and z axes. How can I do it? – Sahabub Jahedi Apr 13 '21 at 07:27
  • @SabatJahedi. You are right: the ranges of the variables are not in need. I added it to my answer. – user64494 Apr 13 '21 at 08:52
  • Maximize[z, Rationalize[ 200.456 + 2.340*10^10*x^2 + 7.99*10^7*y^2 + y*(2.80*10^(-9) - 1.1735*10^6*z) - 29150.591*z + 1.895*10^6*z^2 + x*(-4.329*10^6 - 9.731*10^7*y + 3.135*10^8*z) == 1, 10^-35], {x, y, z}] // N performs {0.00120867,{x->0.0000845289,y->0.0000603497,z->0.00120867}}. Pay your attention to the corrected equation: 2.340 instead of 2.3 and so on. – user64494 Apr 13 '21 at 09:06
  • Thank you so much. Could you please explain it mathematically? why this 10^{-35} has been taken? For precision?? – Sahabub Jahedi Apr 13 '21 at 10:03
  • The range of z is between Minimize[z, Rationalize[ 200.456 + 2.340*10^10*x^2 + 7.99*10^7*y^2 + y*(2.80*10^(-9) - 1.1735*10^6*z) - 29150.591*z + 1.895*10^6*z^2 + x*(-4.329*10^6 - 9.731*10^7*y + 3.135*10^8*z) == 1, 10^-35], {x, y, z}] // N and Maximize[z, Rationalize[ 200.456 + 2.340*10^10*x^2 + 7.99*10^7*y^2 + y*(2.80*10^(-9) - 1.1735*10^6*z) - 29150.591*z + 1.895*10^6*z^2 + x*(-4.329*10^6 - 9.731*10^7*y + 3.135*10^8*z) == 1, 10^-35], {x, y, z}] // N. Yes, 10^-35 is chosen for precision. For example 10^-15 brings several intervals. – user64494 Apr 13 '21 at 10:12
  • Thank you so much. – Sahabub Jahedi Apr 13 '21 at 12:57
  • Let us continue this discussion in chat. – Sahabub Jahedi Apr 13 '21 at 13:01
2

Just a different way to get the same answers using optimization. For some reason using exact (rational) coefficients allows Mathematica to use Min/Maximize instead of NMin/NMaximize and avoids an error for the $y$-coordinate.

r[x_] := Rationalize[x, 10^(-15)]
f[x_, y_, z_] := 
  r@200.45691061895533 + r@2.340594489462856*^10 x^2 + 
   r@7.997019728083995*^7 y^2 + 
   y (r@2.805368856610765*^-9 - r@1.1735999605619283*^6 z) - 
   r@29150.59199218005 z + r@1.8958172135566808*^6 z^2 + 
   x (-r@4.3293045864756685*^6 - r@9.73117535392215*^7 y + 
      r@3.135471494987312*^8 z);
xMin = First@Minimize[{x, f[x, y, z] <= 1}, {x, y, z}];
xMax = First@Maximize[{x, f[x, y, z] <= 1}, {x, y, z}];
yMin = First@Minimize[{y, f[x, y, z] <= 1}, {x, y, z}];
yMax = First@Maximize[{y, f[x, y, z] <= 1}, {x, y, z}];
zMin = First@Minimize[{z, f[x, y, z] <= 1}, {x, y, z}];
zMax = First@Maximize[{z, f[x, y, z] <= 1}, {x, y, z}];
TableForm[N@{{xMin, xMax}, {yMin, yMax}, {zMin, zMax}},
          TableHeadings -> {{"x", "y", "z"}, {"Min", "Max"}}]

RegionPlot3D[f[x, y, z] <= 1 ,
  {x, xMin, xMax}, {y, yMin, yMax}, {z, zMin, zMax},
  AxesLabel -> {x, y, z}, Mesh -> None, ImageSize -> Medium, 
  PlotPoints -> 50]

enter image description here

A.G.
  • 4,362
  • 13
  • 18
1

Same idea as projection onto Cartesian planes: (Thanks @user64494 for simplification!)

L[x_, y_, z_] = 200.456 + 2.340*10^10*x^2 + 7.99*10^7*y^2 + 
  y*(2.80*10^(-9) - 1.1735*10^6*z) - 29150.591*z + 1.895*10^6*z^2 + 
  x*(-4.329*10^6 - 9.731*10^7*y + 3.135*10^8*z) == 1;

project onto the $x$-axis:

fx[x_] = Reduce[Resolve[Exists[{y, z}, L[x, y, z]], Reals], x, Reals]
(*    0.0000819931 <= x <= 0.000101804    *)

project onto the $y$-axis:

fy[y_] = Reduce[Resolve[Exists[{x, z}, L[x, y, z]], Reals], y, Reals]
(*    -0.0000565762 <= y <= 0.000170076    *)

project onto the $z$-axis:

fz[z_] = Reduce[Resolve[Exists[{x, y}, L[x, y, z]], Reals], z, Reals]
(*    -0.000993936 <= z <= 0.00120867    *)
Roman
  • 47,322
  • 2
  • 55
  • 121
  • 1
    Thank you so much. Could you please explain it mathematically? What are the values of x, y, and z? – Sahabub Jahedi Apr 13 '21 at 10:01
  • 2
    The command Reduce[-9.62227*10^-9 - 0.0001135 y + 1. y^2 <= 0, y, Reals] results in -0.0000565762<=y<=0.000170076 and a warning "Reduce::ratnz: Reduce was unable to solve the system with inexact coefficients. The answer was obtained by solving a corresponding exact system and numericizing the result.". – user64494 Apr 13 '21 at 10:08
  • Just to campare. Minimize[y, Rationalize[ 200.456 + 2.340*10^10*x^2 + 7.99*10^7*y^2 + y*(2.80*10^(-9) - 1.1735*10^6*z) - 29150.591*z + 1.895*10^6*z^2 + x*(-4.329*10^6 - 9.731*10^7*y + 3.135*10^8*z) == 1, 10^-35], {x, y, z}] // N results in {-0.0000565762, {x -> 0.0000918975, y -> -0.0000565762, z -> 0.0000723856}}. – user64494 Apr 13 '21 at 10:15
  • @SahabubJahedi just look up the documentation on Exists and Resolve. The last Reduce is just for simplification. – Roman Apr 13 '21 at 10:19
  • @Roman, Thank you so much. – Sahabub Jahedi Apr 13 '21 at 12:58
1
reg = ImplicitRegion[
   200.456 + 2.340*10^10*x^2 + 7.99*10^7*y^2 + 
     y*(2.80*10^(-9) - 1.1735*10^6*z) - 29150.591*z + 1.895*10^6*z^2 +
      x*(-4.329*10^6 - 9.731*10^7*y + 3.135*10^8*z) == 
    1, {{x, 0.00008, 0.00011}, {y, -0.00011, 0.00022}, {z, -0.0015, 
     0.0015}}];
bd = RegionBounds[reg]
Graphics3D[{{Red, DiscretizeRegion[reg, Method -> "ContourPlot3D"]}, 
  Opacity[.5], 
  HighlightMesh[Cuboid @@ Transpose@bd, 
   Style[{1, {5, 2, 3}}, {Thickness[.02], Red}]]}, 
 BoxRatios -> {1, 1, 1}, Boxed -> False]

{{0.0000819931, 0.000101804}, {-0.0000565762, 0.000170076}, {-0.000993936, 0.00120867}}

enter image description here

cvgmt
  • 72,231
  • 4
  • 75
  • 133
  • Clearly the best answer! What would you change to have a smooth ellipsoid in the graphic? – A.G. Apr 15 '21 at 09:44
  • @A.G. Thanks! But I also don't how to do this, so we have to use Show the Contourplot3D instead of DiscretizeREgion[reg] – cvgmt Apr 15 '21 at 10:50