I am trying to find a fitting function for a multidimensional set of data. I will have to find a fitting function that is always lower (conservative) than the data fitted.
The easiest way is to look for the largest underestimation and add this value to the fit function. But this does not lead to very good fits. I have illustrated this in the following using some random data:
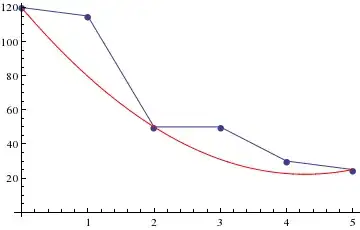
test = {{0.0, 120.0}, {1, 115}, {2, 50}, {3, 50}, {4, 30}, {5, 25}};
function[x_] := a + b x + c x^2;
rep = FindFit[test, function[x], {a, b, c}, {x}]
delta = (test -
Table[{x, function[x]} /. rep, {x, 0, 5, 1}])[[All, 2]];
Show[
ListLinePlot[test, PlotMarkers -> Automatic, AxesOrigin -> {0, 0}],
Plot[function[x] /. rep, {x, 0, 5}, PlotStyle -> Red],
Plot[(function[x] /. rep) + Min[delta], {x, 0, 5},
PlotStyle -> Green]
]

Red is best fit, Green is shifted fit (no longer a good fit).
If I understood correctly I will have to change the norm. But I do not how such a norm could look like and how to implement it. To me it seems like some kind of penalty method could be implemented in the norm.
Thank you very much for your answers and hints!

NonlinearModelFit[], have it return confidence intervals for your parameters for some set confidence level, and take the low ends of those intervals. – J. M.'s missing motivation May 03 '13 at 11:13