31

I have the following set-up:

xaxis = Table[x, {x, 0, 10, 0.01}];

yaxis = Table [Sin[x] + Abs[RandomReal[{-1, 1}]], {x, 0, 10, 0.01}];

ListLinePlot[Transpose[{ xaxis, yaxis}]]

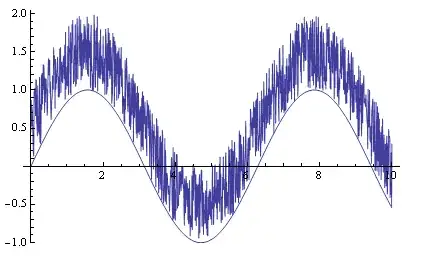
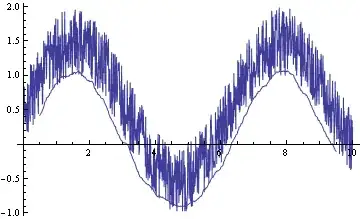
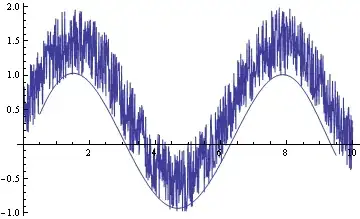
enter image description here

My questions is how can I make a line that very simply envelopes the function coming up from the bottom. The envelope coming up from the bottom should be jagged such that it is a tight-fit (or overfitted). Perhaps this could be controlled by some sort of smoothing parameter where 1: very jagged, 10: very smooth.

The figure below shows a plot generated from the underlying function itself which obviously results in a very smooth fit.

enter image description here

Community
  • 1
akk
  • 1,247
  • 1
  • 15
  • 14

5 Answers5

24

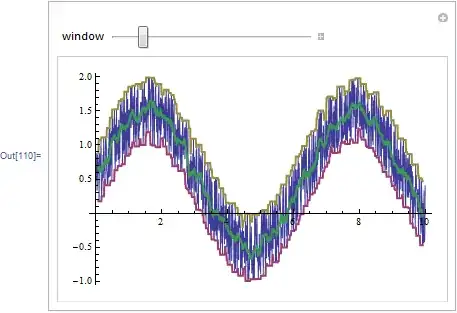
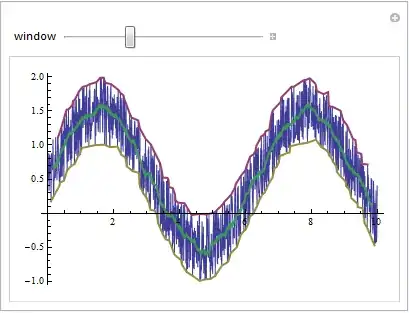
You can also create a moving min (and max) and use BSplineCurve to render a smoothed curve.

These could be made more efficient. They find the min and max over a window.

windowMin[data_, w_][pt_] := {pt, 
  Min[Cases[data, {x_, y_} /; pt - w <= x <= pt + w][[All, 2]]]}

windowMax[data_, w_][pt_] := {pt, 
  Max[Cases[data, {x_, y_} /; pt - w <= x <= pt + w][[All, 2]]]}

This function plots the original data with the BSplineCurve envelope. The parameter w sets the window width.

f[w_] := With[{data = Transpose[{xaxis, yaxis}]}, 
  Show[ListLinePlot[data, 
    PlotStyle -> Directive[{Blue, Opacity[.2]}]], 
   With[{pts = Table[windowMin[data, w][t], {t, 0, 10, w - w/10}]}, 
    Graphics[{Red, BSplineCurve[pts]}]], 
   With[{pts = Table[windowMax[data, w][t], {t, 0, 10, w - w/10}]}, 
    Graphics[{Red, BSplineCurve[pts]}]]]]

Some examples...

f[.2]

enter image description here

f[.1]

enter image description here

f[.025]

enter image description here

Edit: In response to the comment, here is a more general form of f which allows for a list of xdata and a list of ydata provided they are of equal length. The min and max of the Tables are chosen to be the range of the x data.

f[xdata_, ydata_, w_] /; Length[xdata] == Length[ydata] := 
 Block[{data = Transpose[{xdata, ydata}], xmin = Min[xdata], 
   xmax = Max[xdata]}, 
  Show[ListLinePlot[data, 
    PlotStyle -> Directive[{Blue, Opacity[.2]}]], 
   With[{pts = 
      Table[windowMin[data, w][t], {t, xmin, xmax, 
        w - w/(xmax - xmin)}]}, Graphics[{Red, BSplineCurve[pts]}]], 
   With[{pts = 
      Table[windowMax[data, w][t], {t, xmin, xmax, 
        w - w/(xmax - xmin)}]}, Graphics[{Red, BSplineCurve[pts]}]]]]
Andy Ross
  • 19,320
  • 2
  • 61
  • 93
  • This works well however can portion {t, 0, 10, w - w/10} be changed, such that it works with any generic input Table: xaxis, yaxis. – akk Feb 26 '12 at 18:50
  • for instance xaxis can be part of a Table that is obtained from a text file, the function should work provided xaxis and yaxis are the same length – akk Feb 26 '12 at 18:59
  • See my edit. The new version should work for more general x and y data. – Andy Ross Feb 26 '12 at 21:42
  • The function works fine when the data does not have indeterminate values. The issue of indeterminate values is raised in http://mathematica.stackexchange.com/questions/2373/max-of-a-table-list-with-indeterminate-values – akk Feb 27 '12 at 10:17
  • 1
    As you mention, windowMin and windowMax could benefit from the functions MinFilter and MaxFilter. – Matthias Odisio Feb 27 '12 at 14:05
  • With Indeterminate or say Missing[] values I would either drop them or replace them with some sensible value if you have some reason to believe you know what that should be. – Andy Ross Feb 27 '12 at 15:16
12

Here is a method you may be able to use.

The first part plots the lower 1.4 standard deviation over a moving average, and the second part makes a polynomical fit.

xaxis = Table[x, {x, 0, 10, 0.01}];
yaxis = Table[Sin[x] + Abs[RandomReal[{-1, 1}]], {x, 0, 10, 0.01}];
plot = ListLinePlot[Transpose[{xaxis, yaxis}]];
n = 100;
part = Partition[Transpose[{xaxis, yaxis}], n, 1];
dNeg[x_List] := {Mean[x[[All, 1]]],
   Mean[#] - 1.4*StandardDeviation[#] &@x[[All, 2]]};
d = dNeg /@ part;
env = ListLinePlot[d];
Show[{plot, env}]

enter image description here

d2 = Fit[d, {1, x, x^2, x^3, x^4, x^5, x^6}, x];
Show[{plot, Plot[d2, {x, d[[1, 1]], d[[-1, 1]]}]}]

enter image description here

Chris Degnen
  • 30,927
  • 2
  • 54
  • 108
  • This method works well, however the bottom envelope must be such that it envelopes all points. – akk Feb 26 '12 at 16:18
  • Furthermore this method is somewhat tied to the way the data was generated, i.e. a uniform spacing away from the mean. The function should work for any noisy data, which just simply envelopes the lower half. – akk Feb 26 '12 at 21:00
  • @ akk - The spacing (1.4 std dev) varies with the moving average selection. The selection length is set to n = 100 data points in the example. – Chris Degnen Feb 26 '12 at 21:35
  • This method is good！ but… why does the 1.4 standard deviation work? I mean… what's the theoretical basis of this method? – xzczd Mar 28 '13 at 09:07
  • @xzczd - hi, the 1.4 was arbitrarily chosen, by trial & error, as it seemed to give a good fit. – Chris Degnen Mar 28 '13 at 10:26
12

One possibility is going through the data with a window, and selecting the minimum or maximum value. I'm showing code only for the case where the points are equally spaced along the $x$ axis:

Manipulate[
 ListLinePlot[
  {data,
   {Mean[#[[All, 1]]], Min[#[[All, 2]]]} & /@ 
    Partition[data, window, 
     1], {Mean[#[[All, 1]]], Max[#[[All, 2]]]} & /@ 
    Partition[data, window, 1], Mean /@ Partition[data, window, 1]},
  PlotStyle -> {Thin, Thick, Thick, Thick}],
 {window, 1, 100, 1}]

Mathematica graphics

Another possibility is selecting the actual minimum/maximum points instead of taking the average for the $x$ coordinate:

MaxBy[list_, fun_] := list[[First@Ordering[fun /@ list, -1]]]
MinBy[list_, fun_] := list[[First@Ordering[fun /@ list, 1]]]

Manipulate[
 ListLinePlot[
  {data,
   MaxBy[#, Last] & /@ Partition[data, window, 1], 
   MinBy[#, Last] & /@ Partition[data, window, 1], 
   Mean /@ Partition[data, window, 1]},
  PlotStyle -> {Thin, Thick, Thick, Thick}],
 {window, 1, 100, 1}]

Mathematica graphics

Szabolcs
  • 234,956
  • 30
  • 623
  • 1,263
  • this method works fine, could it also be done such that the number of points remain constant, that is the average is taken over each point for a window to the left or right? – akk Feb 27 '12 at 08:58
  • @akk Yes, Andy has already done this, so I didn't change mine further. Is there any reason you don't use Andy's function? It's the same as mine except he wasn't lazy to implement the windowing properly. – Szabolcs Feb 27 '12 at 09:09
  • Right, I was having trouble with the xmin and xmax constructs as some of my data is indeterminate. Looking for a workaround. – akk Feb 27 '12 at 09:48
6

Given enough time, they will take all the fun tasks and make built-in functions out of them. To that end, we can use EstimatedBackground to easily find the envelope on either side of this noisy data:

Manipulate[
 ListLinePlot[{yaxis,
   EstimatedBackground[yaxis, y],
   -EstimatedBackground[-yaxis, y]},
  DataRange -> MinMax@xaxis],
 {y, 1, 20, .1, Appearance -> "Open"}]

enter image description here

Jason B.
  • 68,381
  • 3
  • 139
  • 286
1

If the data is equally distributed, use MaxFilter and MinFilter. Compared to Andy's answer it is much faster. I always try to avoid Cases as it is very slow. Apart from that is does essentially the same thing, with the difference that the radius window is given in data points rather than a radius given by the $x$-axis.

Community
  • 1
CoolKau
  • 11
  • 2