Free vibrations of square plate with bi-harmonic equation

Question

I am still playing with the wave bi-harmonic equation. My question is very similar to another question I posted few weeks ago on this site (Solving rectangular plates vibrations wave equation). I want to visualize the free vibrations of a steel square plate measuring [-a,a;-b,b] and thickness = h (origin = center of the plate).

The issue I met today is the following one : the bi-harmonic equation I am using to NDSolve my problem is working only with some initial conditions parameters sets. With other sets, the computation is never ending (or maybe too long, I don't know) and I get error messages like "DSolve::mxsst: Using maximum number of grid points 100 allowed by the MaxPoints or MinStepSize options for independent variable x." Idem for y and z.

Of course, I searched and found some explanations on this site and some others, but the given solutions never work for me. I think my problem is a method tuning matter in NDSolve. Too hard for me. Help. Thanks in advance.

Below is my code with some helping comments :

(* Free vibrations of square plate *)
Remove["Global`*"]; // Quiet
Needs["DifferentialEquations`NDSolveProblems`"]; 
Needs["DifferentialEquations`NDSolveUtilities`"];
Needs["NDSolve`FEM`"];
Ey = SetPrecision[2.078*10^11, Infinity];(*N/m^2*)
\[Nu] = Rationalize[0.317756];(*unitless*)
\[CurlyRho]d = 8166;(*kg/m^3*)
h = 1/1000;
Df = (Ey h^3)/(12 (1 - \[Nu]^2)); a = 1; b = 1;
eqn = {D[u[x, y, t], {x, 4}] + 2 D[u[x, y, t], {x, 2}, {y, 2}] + 
    D[u[x, y, t], {y, 4}] + (\[CurlyRho]d h)/
     Df D[u[x, y, t], {t, 2}] == 
   0}; (* for plates, governing equation = bi-harmonic equation *)
m = 1; n = 2;
ic = {u[x, y, 0] == 
   Cos[m \[Pi] x/a] Cos[n \[Pi] y/b] + 
    Cos[n \[Pi] x/a] Cos[m \[Pi]  y/b], 
  Derivative[0, 0, 1][u][x, y, 0] == 0}; (* initial impulse *)
bc1fe = {Derivative[2, 0, 0][u][-a, y, t] == 0, 
  Derivative[3, 0, 0][u][-a, y, t] == 0, 
  Derivative[2, 0, 0][u][a, y, t] == 0, 
  Derivative[3, 0, 0][u][a, y, t] == 
   0}; (* free edges/ simplified *)
bc2fe = {Derivative[0, 2, 0][u][x, -b, t] == 0, 
  Derivative[0, 3, 0][u][x, -b, t] == 0, 
  Derivative[0, 2, 0][u][x, b, t] == 0, 
  Derivative[0, 3, 0][u][x, b, t] == 
   0}; (* free edges/ simplified *)
numsol = NDSolve[{eqn, ic, bc1fe, bc2fe}, 
  u, {x, -a, a}, {y, -b, b}, {t, 0, 1}, 
  Method -> {"StiffnessSwitching"}, 
  MaxSteps -> 10^6] (* must show the plate behavior in time *)
(* Results visualization *)
uu[x_, y_, t_] := u[x, y, t] /. numsol;
ListAnimate[
 Table[ContourPlot[Evaluate[uu[x, y, t] == 0], {x, -a, a}, {y, -b, b},
    PlotLabel -> Style[t, 30, Bold]], {t, 0, 1, .05}]]
(* some helping comments:
 )
( I also tried the following possibilities without any success : )
( numsol=NDSolve[{eqn,ic,bc1fe,bc2fe},u,{x,-a,a},{y,-b,b},{t,0,1},

Method[Rule]{"MethodOfLines","SpatialDiscretization"[Rule]{

"TensorProductGrid","MaxPoints"[Rule]101}}]*)
(* numsol=NDSolve[{eqn,ic,bc1fe,bc2fe},u,{x,-a,a},{y,-b,b},{t,0,1},

Method[Rule]{"MethodOfLines","TemporalVariable"[Rule]t,

"SpatialDiscretization"[Rule]"FiniteElement"}] *)
(* one important thing : if I replace " Cos[m [Pi] x/a] Cos[n [Pi] 

y/b]+Cos[n [Pi] x/a] Cosm [Pi/b]" by " Cos[1 x] Cos[3 

y]+Cos[3x] Cos[1y] " the resolution is working well and relatively fast. )
( No error messages hapening *)

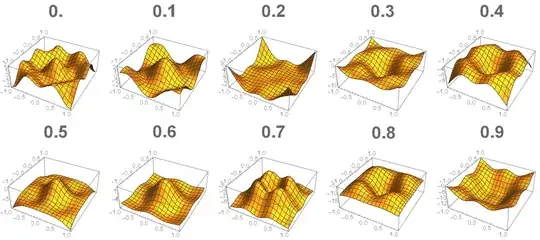
Hereafter is the computation result for Cos[1 x] Cos[3y]+Cos[3x] Cos[1y]. It is also working well for Cos[1 x] Cos[2y]+Cos[2x] Cos[1y]:

Answer 1

Several issues here:

1. Since ibcinc warning pops up and you b.c.s all involve derivative, manual adjustion of "DifferentiateBoundaryConditions" option discussed in this post is necessary.

2. Certain silent change (backslide?) has happened on the ODE solver of NDSolve in recent versions of Mathematica. When the spatial grid is not too dense, v8.0.4 can handle the problem without adjustion of the ODE solver:

   

   but it's not the case for v12.2. One possible work-around I find is to explicitly set Method -> Adams.

The following is the fixed code for v12.2. jianshi is modified from the tools in this post:

showStatus[status_]:=LinkWrite[$ParentLink,
  SetNotebookStatusLine[FrontEnd`EvaluationNotebook[],ToString[status]]];
clearStatus[]:=showStatus[""];
clearStatus[]
jianshi[t_]:=EvaluationMonitor:>showStatus["t = "<>ToString[CForm[t]]]
mol[n:Integer|{_Integer..}, o:"Pseudospectral"] := {"MethodOfLines", 
  "SpatialDiscretization" -> {"TensorProductGrid", "MaxPoints" -> n, 
    "MinPoints" -> n, "DifferenceOrder" -> o}}
mol[tf:False|True,sf_:Automatic]:={"MethodOfLines",
"DifferentiateBoundaryConditions"->{tf,"ScaleFactor"->sf}}
numsol = NDSolveValue[{eqn, ic, bc1fe, bc2fe}, u, {x, -a, a}, {y, -b, b}, {t, 0, 1}, 
    Method -> Union[mol[25, 4], mol[True, 100], {Method -> Adams}], jianshi[t], 
    MaxSteps -> Infinity]; // AbsoluteTiming
(* {61.7096, Null} *)
Table[
 Plot3D[numsol[x, y, t], {x, -a, a}, {y, -b, b}, PlotLabel -> Style[t, 30, Bold], 
  PlotRange -> All], {t, 0, 1, .1}] // Partition[#, 5]& // Grid

Don't be worried about the eerri and eerr warnings, they're merely warnings in this case.