I have a bunch of data points (copied from Mathematica below), which I have 'ListPlotted'
I would now like to compute the Fourier series of this function (after doing a Fourier transform I assume? Or could I do it without?)
This video here (https://www.youtube.com/watch?v=VF1tOcEVGyU) describes how to do the Fourier series on Mathematica for a simpler function. Obviously my data is more complicated so I essentially need a modified version of that (with the slider and other paraphernalia if possible). Would anyone be able to help me please?
Many thanks!
Data:
{{0.30383`,-0.06683`},{0.30837`,-0.05289`},{0.3129`,-0.01927`},{0.31744`,0.02776`},{0.32197`,0.07177`},{0.32651`,0.08597`},{0.33104`,0.06693`},{0.33558`,0.03273`},{0.34011`,0.01049`},{0.34465`,-0.00002`},{0.34918`,0.00341`},{0.35372`,0.01329`},{0.35825`,0.03038`},{0.36279`,0.04189`},{0.36732`,0.04932`},{0.37186`,0.05579`},{0.37639`,0.06438`},{0.38093`,0.05812`},{0.38546`,0.04418`},{0.39`,0.03288`},{0.39454`,0.01151`},{0.39907`,-0.00437`},{0.40361`,-0.02415`},{0.40814`,-0.04318`},{0.41268`,-0.04488`},{0.41721`,-0.02499`},{0.42175`,0.00254`},{0.42628`,0.01371`},{0.43082`,-0.00089`},{0.43535`,-0.03078`},{0.43989`,-0.06009`},{0.44442`,-0.06483`},{0.44896`,-0.04092`},{0.45349`,-0.00142`},{0.45803`,0.03525`},{0.46256`,0.06063`},{0.4671`,0.05745`},{0.47163`,0.02872`},{0.47617`,-0.01207`},{0.4807`,-0.03938`},{0.48524`,-0.04251`},{0.48977`,-0.0247`},{0.49431`,-0.009`},{0.49884`,-0.00429`},{0.50338`,-0.00654`},{0.50791`,-0.01283`},{0.51245`,-0.02396`},{0.51698`,-0.04457`},{0.52152`,-0.0575`},{0.52605`,-0.06183`},{0.53059`,-0.04522`},{0.53512`,-0.01328`},{0.53966`,0.01694`},{0.5442`,0.0262`},{0.54873`,0.00785`},{0.55327`,-0.03305`},{0.5578`,-0.07145`},{0.56234`,-0.07393`},{0.56687`,-0.04686`},{0.57141`,0.00009`},{0.57594`,0.05439`},{0.58048`,0.09047`},{0.58501`,0.09511`},{0.58955`,0.06786`},{0.59408`,0.02886`},{0.59862`,0.00175`},{0.60315`,-0.00192`},{0.60769`,0.00267`},{0.61222`,0.01544`},{0.61676`,0.02639`},{0.62129`,0.03836`},{0.62583`,0.04916`},{0.63036`,0.05637`},{0.6349`,0.0626`},{0.63943`,0.0534`},{0.64397`,0.03629`},{0.6485`,0.02514`},{0.65304`,0.01249`},{0.65757`,-0.00627`},{0.66211`,-0.03374`},{0.66664`,-0.04942`},{0.67118`,-0.04779`},{0.67571`,-0.01435`},{0.68025`,0.02502`},{0.68478`,0.0331`},{0.68932`,0.00401`},{0.69385`,-0.04798`},{0.69839`,-0.08141`},{0.70293`,-0.07461`},{0.70746`,-0.03212`},{0.712`,0.01405`},{0.71653`,0.04915`},{0.72107`,0.06183`},{0.7256`,0.05272`},{0.73014`,0.0145`},{0.73467`,-0.03144`},{0.73921`,-0.05627`},{0.74374`,-0.05574`},{0.74828`,-0.02717`},{0.75281`,-0.00601`},{0.75735`,-0.00398`},{0.76188`,-0.01257`},{0.76642`,-0.02248`},{0.77095`,-0.03554`},{0.77549`,-0.0496`},{0.78002`,-0.06364`},{0.78456`,-0.06266`},{0.78909`,-0.03919`},{0.79363`,-0.0006`},{0.79816`,0.02892`},{0.8027`,0.03215`},{0.80723`,0.00253`},{0.81177`,-0.04562`},{0.8163`,-0.07599`},{0.82084`,-0.07419`},{0.82537`,-0.05056`},{0.82991`,-0.00299`},{0.83444`,0.05197`},{0.83898`,0.10865`},{0.84351`,0.11243`},{0.84805`,0.07439`},{0.85259`,0.02044`},{0.85712`,-0.01928`},{0.86166`,-0.00368`},{0.86619`,0.01589`},{0.87073`,0.03173`},{0.87526`,0.04347`},{0.8798`,0.04385`},{0.88433`,0.03303`},{0.88887`,0.04548`},{0.8934`,0.05886`},{0.89794`,0.06039`},{0.90247`,0.04287`},{0.90701`,0.02219`},{0.91154`,-0.00273`},{0.91608`,-0.03202`},{0.92061`,-0.0581`},{0.92515`,-0.06343`},{0.92968`,-0.02274`},{0.93422`,0.0233`},{0.93875`,0.04349`},{0.94329`,0.03219`},{0.94782`,-0.01951`},{0.95236`,-0.06641`},{0.95689`,-0.08619`},{0.96143`,-0.05603`},{0.96596`,-0.00578`},{0.9705`,0.03317`},{0.97503`,0.05275`},{0.97957`,0.06389`},{0.9841`,0.0474`},{0.98864`,0.01771`},{0.99317`,-0.0187`},{0.99771`,-0.04519`},{1.00224`,-0.05988`},{1.00678`,-0.04695`},{1.01132`,-0.0249`},{1.01585`,-0.01576`},{1.02039`,-0.00908`},{1.02492`,-0.00662`},{1.02946`,-0.01133`},{1.03399`,-0.031`},{1.03853`,-0.05694`},{1.04306`,-0.07548`},{1.0476`,-0.06537`},{1.05213`,-0.02977`},{1.05667`,0.01939`},{1.0612`,0.04822`},{1.06574`,0.05559`},{1.07027`,0.01795`},{1.07481`,-0.04487`},{1.07934`,-0.09278`},{1.08388`,-0.10891`},{1.08841`,-0.06972`},{1.09295`,-0.0061`},{1.09748`,0.05778`},{1.10202`,0.10905`},{1.10655`,0.13207`},{1.11109`,0.10486`},{1.11562`,0.04554`},{1.12016`,-0.00958`},{1.12469`,-0.04035`}}
EDIT: I've been told this is useful info to include! From the comments down below:
"If I saw correctly, that video is about Fourier integrals. Since you have data points, a discrete FT seems more appropriate. Maybe if you explained what is the underlying problem you wish to solve, someone could give better advice. I know how to do some things with the folded points I showed (e.g. smoothing), but the validity of such operations might be questionable. – Daniel Lichtblau
@DanielLichtblau - thanks - ultimately my goal is to analyse this sound wave from my violin to see what is going on. I might then investigate what happens at a particular transition note, though I still haven’t ironed out the details! I’m basically investigating/modelling the sound wave of my violin to see if I can make any interesting observations/comments.
That's useful information. For one, it indicates that trigs are sensible to use, periodicity is present, etc. It also means you might get advice from people familiar with the acoustics of bowed string instruments.

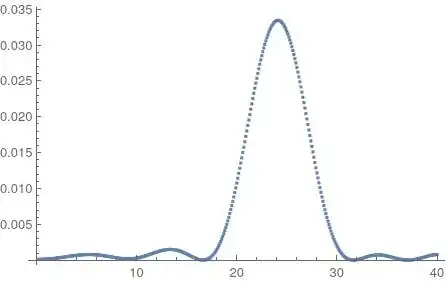
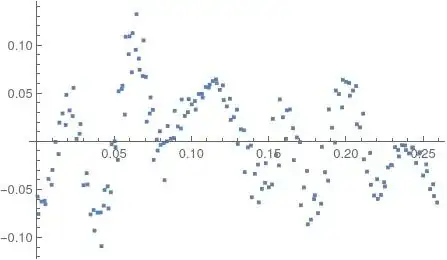


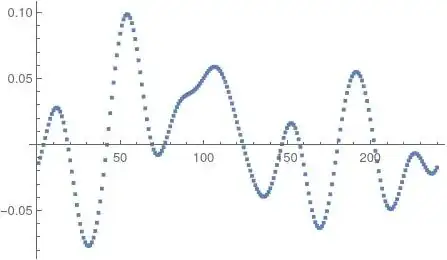


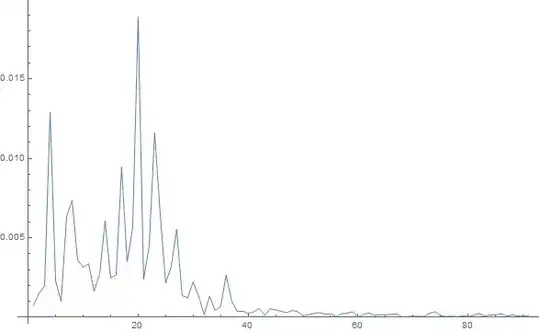






FitandLinearModelFit. – John Doty Jun 03 '21 at 15:15