Finding the periodicity (or wavelength) in approximately periodic data irregularly sampled

Question

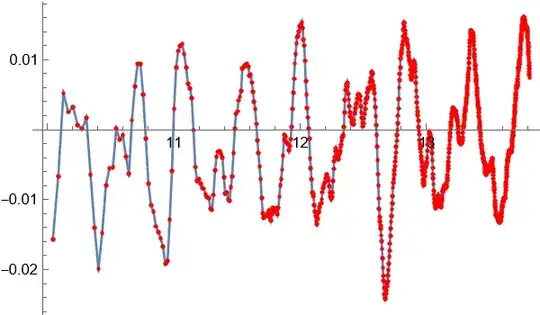
I have irregularly sampled data that looks as in the picture.

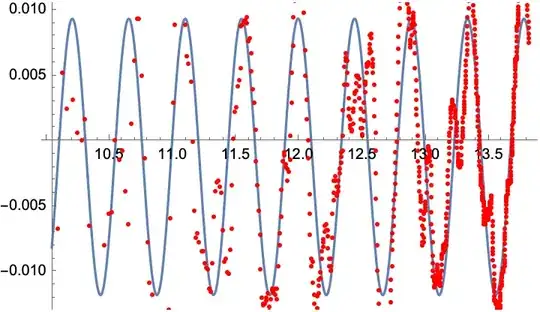
Is there a function in Mathematica that allows me to find an approximate or average period or wavelength?

I know beforehand that the data will always look like this, with some random wiggling.

If there is no function that does this, how best to do it in Mathematica?

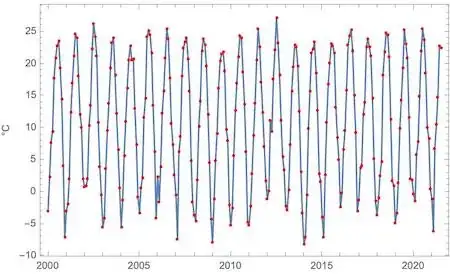
This is a link to the data. The data is very sparse at the beginning and grows denser towards the end. Use ListLinePlot rather than ListPlot to visualize:

https://www.wolframcloud.com/obj/egarcia/Published/M%20STACK%20DATA%202022%20may%2025.nb

data=Import["https://pastebin.com/raw/JvUgqjxT"]

EDIT It is hard to choose a best solution. Perhaps D. Lichtbau's solution using the irregular periodogram function in the function repository I like the most, but I also very much like the fitting solution, as it returns all the parameters needed to make a visual check of the hypothesized periodicity of the data. And as remarked by Roman in a comment, perhaps the best is to use these two in combination. For the sake of just choosing one, I will choose Daniel Lichtbau's solution, perhaps because it is the closest thing to having a function within the Wolfram Language that does what we want.

Answer 1

This is something one can tackle using an irregular periodogram, and that happens to be available in the Wolfram Function Repository.

Grab the data and separate into times and values.

data = Import["https://pastebin.com/raw/JvUgqjxT"];
{times, vals} = Transpose[data];

Plot a periodogram. From picture in the post, guessing we should go to frequency as high as 25.

pgram = Plot[
  ResourceFunction["IrregularPeriodogram"][w, times, vals], {w, 0., 
   25}, PlotRange -> All]

So we see a peak in the vicinity of 14. We can home in on that.

{max, freq} = 
 FindMaximum[
  ResourceFunction["IrregularPeriodogram"][w, times, vals], {w, 14}]
(* Out[23]= {0.0284429, {w -> 14.0784}} *)

the approximated period can be computed from this.

per = 2*Pi/w /. freq
(* Out[24]= 0.4463 *)

Another way to approximate the period, directly in this case, is to use the Lafler-Kinman (or string length) method.

pgramLK = 
 Plot[ResourceFunction["IrregularPeriodogram"][w, times, vals, 
   Method -> "LaflerKinman"], {w, 0., 1}, PlotRange -> All]

Now we can minimize this to approximate the period. Here I use NMinimize to get around a problematic gradient computation. As there are two dips (indicating we might have to halve the main frequency) we'll compute both.

{min, per} = 
 NMinimize[
  ResourceFunction["IrregularPeriodogram"][w, times, vals, 
   Method -> "LaflerKinman"], {w, .4, .45}]
(* Out[34]= {5.17042, {w -> 0.447938}} *)
{min2, per2} = 
 NMinimize[
  ResourceFunction["IrregularPeriodogram"][w, times, vals, 
   Method -> "LaflerKinman"], {w, .85, .95}]
(* Out[43]= {3.62404, {w -> 0.888249}} *)

Check that they are approximately consistent.

w/2 /. per2
(* Out[45]= 0.444125 *)

I will remark that I trust more the default method, in the sense that it gives no indication of lower frequency peak near 7.07.

Answer 2

Maybe a nonlinear fit would work for you, but it needs a good starting point to converge:

f = NonlinearModelFit[data,
                      a + b Sin[c x + d],
                      {{a, 0}, {b, 0.01}, {c, 14}, {d, 2.5}},
                      x];
f["BestFitParameters"]
(*    {a -> -0.00119216, b -> 0.0105601, c -> 14.0715, d -> 2.47229}    *)
Plot[f[x], {x, Sequence @@ MinMax[data[[All, 1]]]}, Epilog -> {Red, Point[data]}]

Answer 3

Try using Periodogram. See for more HERE. In short on an example, let's take temperature data - about 2 decades, sampling monthly:

temp=WeatherData["Chicago","Temperature",{{2000,1,1},{2021,6,31},"Month"}];

You got something pretty periodic, but not exactly periodic:

DateListPlot[temp,FrameLabel->Automatic,Mesh->All,MeshStyle->Red]

Now Periodogram picks frequency related to 1-year period easily with a peak at 1:

Periodogram[QuantityMagnitude[Values@temp],
SampleRate->12,
PlotRange->All,Frame -> True,AspectRatio -> 1/3,
GridLines -> {{1}, None}, 
GridLinesStyle -> Directive[Red,Thick, Dashed]]

Ignore first peak at zero, it is probably related to the fact that the data have none-zero average. To understand why this works option SampleRate->12 is important. Your data basically are something like transformation of a basic function similar to

Sin[2 Pi / (1 year)]

so your frequency is 1 and you sample with a month meaning 1/12-th of a year.

Answer 4

To get an equal distant sampling you can use Interpolation and resample (assuming your data is stored in "data" and I eliminate the x values because they are not important for frequencies for equidistant data points):

dat = Table[int[x], {x, 10.05, 13.8, 0.01}];
ListPlot[dat]

If we now get the periodogram we see that there is no dominant frequency.

Periodogram[dat, PlotRange -> All]