TL;DR
How to implement in mathematica a tool such as WebPlotDigitizer by Ankit Rohatgi which would allow us to trace automatically curves from either (randomly ordered) data or imported images.
Context
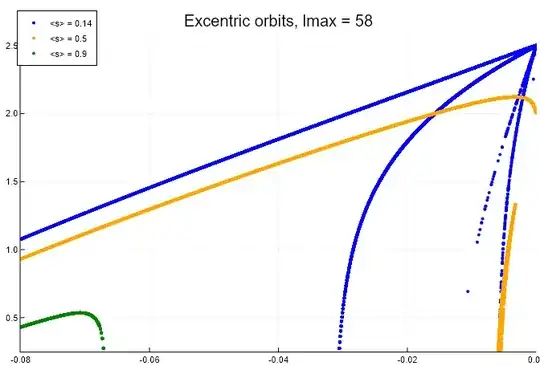
As a Follow up of this question and both nice answers given there, I am after an algorithm which could (as automatically as possible) trace the different sets of curves in plots such as these (calorific curves of distribution of intermediate black holes in a Galactic centre).
The challenge is that these points are found by some complex optimisation routine and are over-numerous in places. So I am interested in resampling the different curves. Note importantly that the curves cross (e.g. near (-0.015,2)). This can be seen as a reverse engineering problem to extract a compact re-parametrisation of the different curves (hence the link to WebPlotDigitizer).
Question
How can one achieve the automatic curve matching/ sampling procedure?
Attempt
Let me define a toy problem as follows: let me produce two curves:
data = Flatten[{Table[{x, Sin[x^2/15]}, {x, 0, 20, 0.01}],
Table[{x, 1 + Cos[x]}, {x, 0, 20, 0.1}]}, 1];
and draw random points from those.
pts = RandomChoice[data, Length[data]];
ListPlot[pts]
Note that on purpose the sampling is not the same for the two curves.
One could imaging one of two situations: either have access to pts or ListPlot[pts]//Image (but obviously not data).
Following this (excellent) answer I can get a good resampling as follows:
tour = Last[FindShortestTour[pts]];
tourPts = Extract[pts, List /@ tour];
peaks = Ordering[EuclideanDistance @@@ Partition[tourPts, 2, 1], -2];
{firstCurve, secondCurve} =
TakeDrop[RotateLeft[tourPts, peaks[[1]]], Abs[Subtract @@ peaks]];
np[f_][u_, dt_] := u + dt/Norm[f'[u]]
equallySpacedPts[pts_, dt_] :=
With[{bsf = BSplineFunction[pts]},
bsf /@ Most[NestWhileList[np[bsf][#, dt] &, 0, # < 1 &]]]
equallySpacedPts[#,0.25]&/@{firstCurve,secondCurve}//ListLinePlot
BUT It is clear that the two curves are not (always) properly matched, e.g. near x=3 or x=15.
I understand that this is not a trivial matter, but it should be IMHO of general interest for mathematica to be able to stand up to this challenge with minimum manual input (?).
Comment:
It might be possible to use a R package via digitizeR and R integration in Mathematica, but obviously a standalone implementation would be preferable.



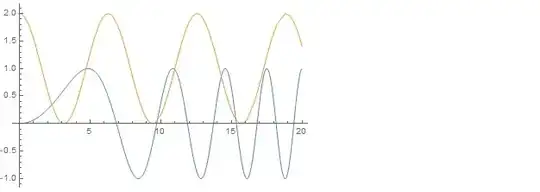
data = Flatten[{Table[{x, Sin[x^2/15]}, {x, 0, 20, 0.01}], Table[{x, 1 + Cos[x]}, {x, 0, 20, 0.1}]}, 1];– chris Jul 13 '21 at 05:36