Connecting simple lines from (large) unsorted list of points

Question

Context

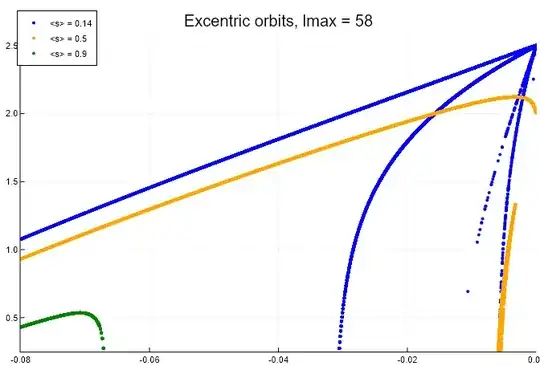
We are trying to predict the formation of discs of intermediate mass black hole orbiting super massive black holes in galactic centres. This involves finding calorific curves in energy and angular momentum space.

Problem

I am trying to identify sets of curves from a (very large) sets of points in order to produce a lighter figure.

For instance I want to be able to redo such figure, but with less points (without loosing the poorly sampled lines).

The challenge is that these points are found by some complex optimisation routine and are over-numerous in places. So by lighter figure, I mean remove sets of point very close to each other while keeping more sparsely sampled points in order to draw curves through them.

Question

How can one achieve this simultaneous downsampling and curve matching procedure?

---

Attempt

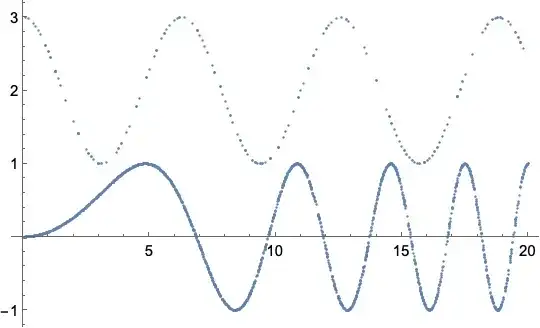
Let me define a toy problem as follows: let me produce two curves:

data = Flatten[{Table[{x, Sin[x^2/15]}, {x, 0, 20, 0.01}],
    Table[{x, 2 + Cos[x]}, {x, 0, 20, 0.1}]}, 1];

and draw random points from those.

pts = RandomChoice[data, Length[data]];
ListPlot[pts]

Note that on purpose the sampling is not the same for the two curves.

---

I found on this site and in the documentation a couple of partial solutions to this problem, but none does both the curve identification and downsampling properly.

The first method relies on Nearest (from the documentation) but does neither job (interpolation or downsampling) particularly well:

p = Nearest[pts];
pts1 = p[#, 2][[2]] & /@ pts;
Graphics[{Line[{##}] & @@@ Transpose[{pts, pts1}]}, Axes -> True, 
 AspectRatio -> 2/3]

From this answer I tried also ListCurvePathPlot which seems like a good start but does not down sample.

pl = ListCurvePathPlot[pts, Mesh -> All, 
  MeshStyle -> Directive[ColorData[97][2], PointSize[Large]],
  AspectRatio -> 1]

Finally FindShortestTour doesnt do as good a job, but lets me downsample by brute force (which is clearly sub optimal).

---

ListLinePlot[pts[[FindShortestTour[pts][[2]][[;; ;; 20]]]], 
 PlotMarkers -> {Automatic, 10}, InterpolationOrder -> 1]

---

I am optimistic that this question has a Mathematica answer since it can be done by hand relatively easily (?)

Answer 1

Here is a way to downsample based on the distance between points. I use Manipulate to adjust the threshold that reduces the number of points. As the $x$ and $y$ axes are on different scales it is probably better to scale before taking euclidean distances, as is done in the second example.

SeedRandom[0];
data = Flatten[{Table[{x, Sin[x^2/15]}, {x, 0, 20, 0.01}], 
    Table[{x, 2 + Cos[x]}, {x, 0, 20, 0.1}]}, 1];
n = Length[data];
pts = RandomChoice[data, n];
(* Eliminate points based on euclidean distance *)
Manipulate[
 p1 = DeleteDuplicates[pts, 
   EuclideanDistance[#1, #2] <= minDistance1 &];
 ListPlot[p1, 
  PlotLabel -> 
   Row[{"Number of points: ", Length@p1, " out of ", n}]],
 {{minDistance1, .1}, 0, 0.25}]
(* Eliminate points based on scaled euclidean distance *)
xRange = With[{x = First /@ pts}, Max@x - Min@x];
yRange = With[{y = Last /@ pts}, Max@y - Min@y];
scaledDistance[{x1_, y1_}, {x2_, y2_}] := 
  Sqrt[(x2 - x1)^2/xRange^2 + (y2 - y1)^2/yRange^2 ];
Manipulate[
 p2 = DeleteDuplicates[pts, 
   scaledDistance[#1, #2] <= minDistance2 &];
 ListPlot[p2, 
  PlotLabel -> 
   Row[{"Number of points: ", Length@p2, " out of ", n}]],
 {{minDistance2, .02}, 0.01, 0.05}]
(* Now add interpolation *)
Manipulate[
 p3 = DeleteDuplicates[pts, 
   scaledDistance[#1, #2] <= minDistance3 &];
 Show[
  ListCurvePathPlot[p3, Mesh -> All, 
   MeshStyle -> Directive[ColorData[97][2], PointSize[Large]], 
   AspectRatio -> 1, 
   PlotLabel -> Row[{"Number of points: ", Length@p3, " out of ", n}]],
  ListPlot[p3, PlotStyle -> {Black, PointSize[0.01]}]],
 {{minDistance3, .02}, 0.01, 0.05}]

Answer 2

Edit: Just noticed @Rom38 essentially mentioned the same approach in the comments above, credit goes to them.

This can be solved as two separate questions: namely separating the points into 'curves' and then down-sampling a list of points.

For the first question, I use FindShortestTour to find a single continuous curve, and then split it up according to EuclideanDistance jumps. I suspect this might need some fine-tuning for different use-cases, but seems to work well for the case of OP:

data = Flatten[{Table[{x, Sin[x^2/15]}, {x, 0, 20, 0.01}],Table[{x, 2 + Cos[x]}, {x, 0, 20, 0.1}]}, 1];
pts = RandomSample[data];
tour = Last[FindShortestTour[pts]];
tourPts = Extract[pts, List /@ tour];
peaks = Ordering[EuclideanDistance @@@ Partition[tourPts, 2, 1], -2];
{firstCurve, secondCurve} = TakeDrop[RotateLeft[tourPts, peaks[[1]]], Abs[Subtract @@ peaks]];

For the second question, there's many related questions on this site, e.g. here and here. I'll use the accepted solution from the first link for demonstration purposes.

np[f_][u_, dt_] := u + dt/Norm[f'[u]]
equallySpacedPts[pts_, dt_] := With[{bsf = BSplineFunction[pts]},
  bsf /@ Most[NestWhileList[np[bsf][#, dt] &, 0, # < 1 &]]]
equallySpacedPts[#, 0.25] & /@ {firstCurve, secondCurve} // ListPlot