NDSolve with vector function

Question

(Possible duplicate yet I still can't understand.)

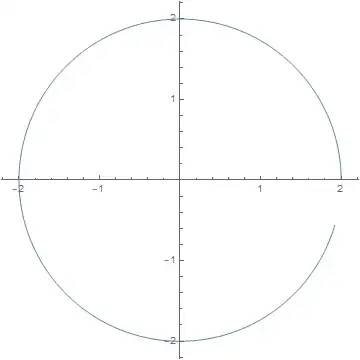
Basic 2D revolving around origin:

With[{o = 2, R = 2},
 NDSolveValue[{
   r''[t] == -o^2 R Normalize[r[t]],
   r[0] == {R, 0},
   r'[0] == {0, o R}},
  r, {t, 0, 3}]]

ParametricPlot[%[t], {t, 0, 3}]

However, I add an origin displacement to rhs of r''[t] and suddenly it can't be solved.

With[{o = 2, R = 2, p = {0, 0}},
 NDSolveValue[{
   r''[t] == -o^2 R Evaluate[Normalize[r[t] - p]],
   r[0] == p + {R, 0},
   r'[0] == {0, o R}},
  r, {t, 0, 3}]]

Errors-filled return of NDSolveValue also shows rhs of r''[t] is evaluated in an undesired fashion. How can I remedy this but still go on with my vector variable?

Answer 1

The problem is that Mathematica prematurely threads r[t] - p not knowing r[t] is actually in $\mathbb{R}^2$

In[]:= r[t] - {0, 0}
Out[]= {r[t], r[t]}

Which is not what you want. A quick fix for these types of issues is to create a function that only evaluates for numerical values (Changed to NDSolve since I only have version 8):

dummy[r_?(VectorQ[#, NumericQ] &), p_] := Normalize[r - p]
With[{o = 2, R = 2, p = {0, 0}},
 NDSolve[
  {r''[t] == -o^2 R dummy[r[t], p], r[0] == p + {R, 0}, r'[0] == {0, o R}},
  r, {t, 0, 3}]
]

Where r_?(VectorQ[#, NumericQ] &) makes sure that the first argument is a list of numbers:

In[]:= dummy[r[t], {0, 0}]
Out[]= dummy[r[t], {0, 0}]
In[]:= dummy[{1., 3.}, {0, 0}]
Out[]= {0.316228, 0.948683}

This ensures that the evaluation of Normalize[r[t] - p] only happens once the solving actually starts, thereby preventing improper threading.

Answer 2

Another useful method for this case is to instead use TranslationTransform[], which sidesteps the premature threading observed in the OP:

With[{o = 2, R = 2, p = {0, 0}}, 
     rf = NDSolveValue[{r''[t] == -o^2 R Normalize[TranslationTransform[-p][r[t]]], 
                        r[0] == p + {R, 0}, r'[0] == {0, o R}}, r, {t, 0, 3}]];
ParametricPlot[rf[t], {t, 0, 3}]