NDSolve with vectors

Question

I'm stumped. I'm trying to write this using vectors, but the 2nd derivative isn't being expanded like I expected it to be. This is a system of equations for a projectile with quadratic drag and gravity (the linear drag is ignored for now). Negative Z is down, X and Y are the horizontal plane. If I write it as 9 equations, one for each coordinate, it works fine, but I'd rather use vectors since it is shorter and (to at least me) more obvious what is going on. Plus since I am new to Mathematica it would be good to learn more/better ways to use it.

gravity = 10;
withDrag[p0_, v0_, drag_] := 
 NDSolve[{
   p[0] == p0,
   p'[0] == v0,
   p''[t] == drag * Norm[p'[t]] * p'[t] + {0,0,-gravity}},
  {p}, {t, 0, 5}]

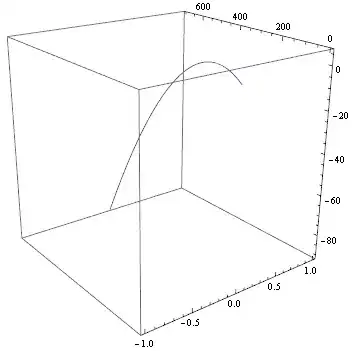
withDrag[{0,0,0}, {0,10^4,10}, 0.001]

I get:

NDSolve::ndfdmc: Computed derivatives do not have dimensionality consistent with the initial conditions. >>

NDSolve[{
  p[0] == {0, 0, 0}, 
  p'[0] == {0, 10000, 10}, 
  p''[t] == {
    0.001 Norm[p'[t]] p'[t], 
    0.001 Norm[p'[t]] p'[t], 
    -10 + 0.001 Norm[p'[t]] p'[t]}}, 
 {p}, {t,0,5}]

I formatted the output to make the error more obvious. Each of elements of the p'' vector has all three elements of p'[t]. Each one should really be p'[t][[dim]] (or something like that).

Any clues as to what I'm doing wrong?

score 16 · Accepted Answer · answered Nov 11 '12 at 20:27

16

Mathematica doesn't have vector variables (yet). That is to say, you can assign a list to a variable, but you cannot use a variable in a function like NDSolve and let Mathematica work out its dimensions or let the dimensions be undetermined.

If you change your function to this:

gravity = 10;
withDrag[p0_, v0_, drag_] :=
 Module[{p},
  p[t_] := {p1[t], p2[t], p3[t]};
  p[t] /.
   NDSolve[
    Thread /@ {
       p[0] == p0,
       p'[0] == v0,
       p''[t] == drag*Norm[p'[t]]*p'[t] + {0, 0, -gravity}} // Flatten,
    p[t],
    {t, 0, 5}
    ]// First
  ]

it works. What is does is defining your p as a vector (list) of functions. Thread takes care of distributing == over the vector components and Flatten makes a single list of equations from all this.

track[t_] = withDrag[{0, 0, 0}, {0, 10^2, 10}, 0.001];

ParametricPlot3D[track[t], {t, 0, 5}, BoxRatios -> 1]

Mathematica graphics

Note that I reduced the starting value of v0[[2]] to 10^2 because 10^4 yields a 'stiff' system. Also note that I used BoxRatios -> 1 to prevent the box from becoming flat.

While under the hood this method still provides Mathematica with the 9 equations that you already tried manually, it has the advantage that it leaves your vector equations intact.

answered Nov 11 '12 at 20:27

Sjoerd C. de Vries

65,815
14
188
323

3

This is also how I would have done it, but it should probably be pointed out that Mathematica does know how to deal with vector functions in some cases. See e.g. this answer. – Jens Nov 11 '12 at 22:04
@jens You're right. I suppose the problem here lies in the assignments with p0 and v0, which aren't explicitly vectors, right? – Sjoerd C. de Vries Nov 11 '12 at 22:27
@jens Vector equations seem to work only if the initial conditions are specified as a scalar constant, not a vector constant. Replace in the doc example the zero in the first example by {0,0,0,0} (which would seem to make more sense) and it fails. – Sjoerd C. de Vries Nov 11 '12 at 22:43
Yes, I guess one could change the function argument from p0_ to {p0x_, p0y_, p0z_} etc., but it seems that even then the second-order differential equation is too hard to recognize as vectorial. So your approach is just the safest, I think. – Jens Nov 11 '12 at 22:45
Nice. I'll have to study the answer some more though... Thanks! – Steve Nov 12 '12 at 21:37
The drag term should be negative as it opposes the motion. I think the stiffness of system stems from here. – BoLe Jul 06 '16 at 06:37

score 16 · Answer 2 · answered Dec 27 '13 at 14:22

As of Version 9, you can work with vectors in NDSolve[]!:

gravity = 10;
withDrag[p0_, v0_, drag_] := Module[{p},
  p[t_] := Evaluate@Array[Unique[][t] &, 3];
  p[t] /. NDSolve[{
                   p[0]   == p0,
                   p'[0]  == v0,
                   p''[t] == drag*Norm[p'[t]]*p'[t] + {0, 0, -gravity}},
               p[t], {t, 0, 5}] // First]

track[t_] = withDrag[{0, 0, 0}, {0, 10^2, 10}, 0.001];
ParametricPlot3D[track[t], {t, 0, 5}, BoxRatios -> 1]

Mathematica graphics

score 2 · Answer 3 · edited Apr 13 '17 at 12:55

Having a helper function rhs, which evaluates only with a numeric vector as argument, for the right-hand side of the force equation lets you use vectors as you want. This way the undesired symbolic precalculation (threading of drag (v.v) Normalize[v] with {0, 0, gravity}) is bypassed and the solving continues numerically. See this answer for a bit more detail.

Physically, the drag term should be negative. Also, just as an interesting angle, I added WhenEvent "equation" that terminates the integration when particle hits the ground.

withDrag[p0_, v0_, drag_] :=
 Module[{gravity = 10, rhs},
  rhs[v_?(VectorQ[#, NumericQ] &)] :=
   -drag (v.v) Normalize[v] - {0, 0, gravity};
  NDSolveValue[{
    p''[t] == rhs[p'[t]],
    p'[0] == v0,
    p[0] == p0,
    WhenEvent[p[t][[3]] < 0, "StopIntegration"]}, 
   p, {t, 0, \[Infinity]}]]

The solution time depends on the initial values, it can be extracted with suitable parting.

sol = withDrag[{0, 0, 0}, {10, 10, 100}, .1];

ParametricPlot3D[sol[t], {t, 0, sol[[1, 1, 2]]},
 BoxRatios -> 1,
 ImageSize -> Small]

I would advise using explicit variables instead of % (Out) as it might store a different thing on someone else's machine if cells are not evaluated in the exact order of your post. — István Zachar, Jul 06 '16 at 07:23
Can you explain how this works? sol[[1, 1, 2]]? Is this extracting the time it hit ground? — user48879, Mar 22 '22 at 01:40

NDSolve with vectors

3 Answers3

Linked