4D ListPlot? How do I plot discrete points (x,y,z,f(x,y,z))? ListDensityPlot3D does not work

Question

I have a discrete dataset data of the form {10524, 2} where I have in the first row the {x,y,z} coordinates and in the second row the evaluation f[x,y,z]. The points are not dense, in that sense, that I kept only some points of $f$ above a bound.

Ignoring $f$ I can do that with ListPointPlot3D[data[[;; , 1]]] however I don't see then, when the function is really large.

Is there a Colouring-Option or a totally different Plot-Option similar to perhaps DensityPlot3D?

So a minimal example,

data = {{{0, 0, 0}, 1}, {{0, 1, 1}, 2}, {{0, 2, 1}, 3}}
ListPointPlot3D[data[[;; , 1]]]

And I want to see the difference between $1,2,3$

Thanks alot in advance

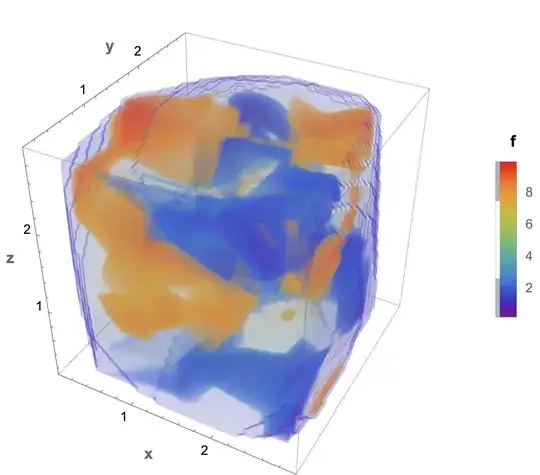
EDIT2: I now found C ListDensityPlot3D` which works for

data2 = {{0, 0, 0, 1}, {0, 1, 1, 2}, {0, 2, 1, 3}, {1, 2, 3, 4}, {0, 
   1, 0, 5}}
ListDensityPlot3D[data2]

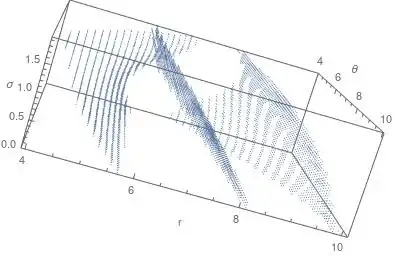
but not doing a picture for my real data2 containing 5000 points, see a ListPointPlot3D below

The reason that ListDensityPlot3D doesn't work on data2 is that it requires the x, y, z coordinates to make up a rectangular array (though the error message generated could be clearer about this.) Try data3 = Flatten[Table[{i, j, k, i + j + k}, {i, 0, 2}, {j, 0, 2}, {k, 0, 2}], 2]; ListDensityPlot3D[data3] for a version that does work. — Michael Seifert, Aug 11 '21 at 15:01
It looks like ListDensityPlot3D requires at least 5 data points: data2 = {{0, 0, 0, 1}, {0, 1, 1, 2}, {0, 2, 1, 3}, {1, 1, 1, 4}, {-1, 1, 1, 3}}; ListDensityPlot3D[data2] works for me, despite not being a rectangular array (contrary to what @MichaelSeifert suggested) — Lukas Lang, Aug 11 '21 at 15:06
@LukasLang: I stand corrected! I was going off the line in the documentation that says "array should be an array of real numbers; positions where array is not a real number are rendered transparently". But on closer inspection this appears to refer to a different usage of ListDensityPlot3D (the usage without coordinates.) — Michael Seifert, Aug 11 '21 at 15:14
This gives a nice visualization of the sample data2, which is quite special since the data is contained in a plane (and mathematically is actually 3D not 4D): data3 = Join[data2, # - {1, 0, 0, 0} & /@ data2, # + {1, 0, 0, 0} & /@ data2]; cfn = "DefaultColorFunction" /. (Method /. ChartingResolvePlotTheme[Automatic, ListSliceDensityPlot3D]) // ColorData; With[{range = MinMax[data3[[All, -1]]]}, ListSliceDensityPlot3D[data3, {"XStackedPlanes", {0.}}, ColorFunction -> (cfn[Rescale[#, range, {0, 1}]] &), ColorFunctionScaling -> False]]` — Michael E2, Aug 11 '21 at 17:20
Dear Michael Seifert, Lukas Land ang Michael E2, thanks for your comments, I did not realize that when creating that minimal example. However as answered to Bob below, my "true" data2 contains 5000 points and I added a picture created with the x,y,z-coordinates to the original postings — Michael Fischer, Aug 12 '21 at 10:20

Bob Hanlon · Answer 1 · 2021-08-11T15:34:57.873

$Version

(* "12.3.1 for Mac OS X x86 (64-bit) (June 19, 2021)" *)

Clear["Global`*"]

data = {{{0, 0, 0}, 1}, {{0, 1, 1}, 2}, {{0, 2, 1}, 3}};

{fmin, fmax} = MinMax[data[[All, 2]]]

(* {1, 3} *)

Legended[
 Graphics3D[
  {AbsolutePointSize[6],
   {ColorData["Rainbow"][Rescale[#[[2]], {fmin, fmax}]],
      Point[#[[1]]]} & /@ data},
  Axes -> True,
  AxesLabel -> (Style[#, 12, Bold] & /@
     {"x", "y", "z"})],
 BarLegend[{"Rainbow", {fmin, fmax}},
  LegendLabel -> Style["f", 12, Bold]]]

EDIT: ListDensityPlot3D works if the data is structured as ListDensityPlot3D[{{x1, y1, z1, f1}, {x2, y2, z2, f2},…}] and there are sufficient number of points. However, "ListDensityPlot3D linearly interpolates values so as to give color changes" and "ListDensityPlot3D is mainly intended for continuous values." Since you describe your data as "discrete" and "not dense" it may not be a good fit to this form of visualization. However, without representative data it is difficult to say.

Clear["Global`*"]
SeedRandom[1234];
data2 = Flatten /@ Table[{RandomReal[{0, 3}, 3], RandomReal[10]}, {200}];
ListDensityPlot3D[data2,
 AxesLabel ->
  (Style[#, 12, Bold] & /@ {"x", "y", "z"}),
 ColorFunction -> "Rainbow",
 PlotLegends -> BarLegend[Automatic,
   LegendLabel -> Style["f", 12, Bold]]]

Hey Bob, thanks alot! will try your code on my big dataset, any idea why ListDensityPlot3D doesn't work? — Michael Fischer, Aug 11 '21 at 14:43
Dear Bob, thanks again for your detailed answer. I understand now that ´data2´ does not contain enough points, however weirdly enough my "real" data2 contains 5000 points and is the discretisation of a manifold, the long time behavior of a PDE, unweighted in ListPoint3D it loos fine and like something easy to interpolate. I'll add it just for information in the main post and will play around with your codes, thank you again very much — Michael Fischer, Aug 12 '21 at 10:17

4D ListPlot? How do I plot discrete points (x,y,z,f(x,y,z))? ListDensityPlot3D does not work

1 Answers1