1

EDIT: I reposted this question, removing everything that is not necessary for my coupling approach. Find the new post here.

I am working on a 3D simulation of the heat equation which is coupled to a 1D simulation of the convective term of the heat equation (flow in a channel). The image below shows the 3D solid and the cutout where the channel is:

geometry

I have been working with a method proposed in an old post. The coupling method in the post works by estimating the wall temperature with a single line along the channel wall. I was testing the energy conservation by applying a Neumann BC to the backside of the solid, but it was about 5% off. The channel wall consists of 9 segments and I tried using the average of multiple lines, but that didn't improve energy conservation enough. See line positions below:

lines

I was able to achive a good energy conservation at about 1E-4% of the incoming heat flux by integrating the average wall temperature along the z-coordinate for a number of nodes and using them to create an interpolating function which I then use as the wall temperature for the 1D simulation. Initiating the integration stuff before the main loop:

(*Integration stuff*)
chanPart[x_, y_, z_][zmin_, zmax_] := 
 zmin <= z <= zmax; (*condition for partial integration over boundary*)

numPieces = 20(numElements);


deltaZ = l/numPieces;


(z coordinates for interpolation function with average temperature 

integration)
tempZs = Table[
   (i + 0.5)*deltaZ
   , {i, 0, numPieces - 1}
   ];
PrependTo[tempZs, 0];
AppendTo[tempZs, l];


(area of integration pieces for averaging temperature)
areaPiece = 
  FEMNBoundaryIntegrate[1, {x, y, z}, bmesh, 
    ElementMarker == 3 || ElementMarker == 4 || ElementMarker == 6 || 
     ElementMarker == 7 || ElementMarker == 9 || ElementMarker == 10 ||
      ElementMarker == 11 || ElementMarker == 12 || 
     ElementMarker == 13]/numPieces;


relLenEndPiece = 
 1/200;(relative length of integration pieces for ends of 

interpolating function of wall temperature)
areaFrontBackPiece = areaPiece * numPieces*relLenEndPiece;

Performing the integration of Tn[i] (Interpolating function of the temperature of the solid from NDSolve of the current iteration) in the main loop (equidistant integration pieces and adding some value for z=0 and z=l for the interpolation function):

(*##### Integration wall temperature function ####*)
integrateTime = First@Timing[

(partially integrate channel surface)
   temps = Table[
     FEMNBoundaryIntegrate[
       Piecewise[{{Tn[i][x, y, z], 
          chanPart[x, y, z][numdeltaZ, (num + 1)deltaZ]}, {0, 
          True}}],
       {x, y, z}, bmesh, 
       ElementMarker == 3 || ElementMarker == 4 || 
        ElementMarker == 6 || ElementMarker == 7 || 
        ElementMarker == 9 || ElementMarker == 10 || 
        ElementMarker == 11 || ElementMarker == 12 || 
        ElementMarker == 13]/areaPiece
     , {num, 0, numPieces - 1}];


(add values for z=0 and z=l)
   PrependTo[temps,
    FEMNBoundaryIntegrate[
      Piecewise[{{Tn[i][x, y, z], 
         chanPart[x, y, z][0, l*relLenEndPiece]}, {0, True}}],
      {x, y, z}, bmesh, 
      ElementMarker == 3 || ElementMarker == 4 || ElementMarker == 6 ||
        ElementMarker == 7 || ElementMarker == 9 || 
       ElementMarker == 10 || ElementMarker == 11 || 
       ElementMarker == 12 || ElementMarker == 13]/areaFrontBackPiece
    ];
   AppendTo[temps,
    FEMNBoundaryIntegrate[
      Piecewise[{{Tn[i][x, y, z], 
         chanPart[x, y, z][l(1 - 1relLenEndPiece), l]}, {0, True}}],
      {x, y, z}, bmesh, 
      ElementMarker == 3 || ElementMarker == 4 || ElementMarker == 6 ||
        ElementMarker == 7 || ElementMarker == 9 || 
       ElementMarker == 10 || ElementMarker == 11 || 
       ElementMarker == 12 || ElementMarker == 13]/areaFrontBackPiece
    ];
(associate average temperature values to z coordinates)
 tempPointsZ = Transpose[{tempZs, temps}];


(create actual wall temperature function)
 tempIntegrateInterpFun = 
   Interpolation[tempPointsZ, InterpolationOrder -> 2];
 ];(End Timing Integration)

The following plot compares the different approaches of estimating the average wall temperature as a function of the z coordinate. Note that TwAlt is the original from the aforementioned post. The dots are the averaged temperatures at different points by integration and tempIntergrateInterpFun is the interpolation function created by the points.

tws

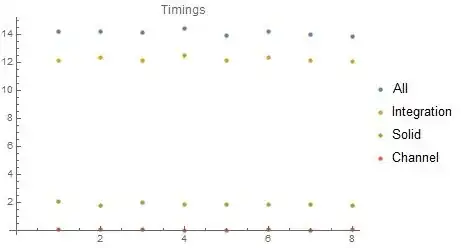
This approach achieves good results, but the integration of the average wall temperature takes up most of the calculation time. See the plot below comparing the time consumption per iteration.

times

I want to use this approach for simulations that take about 5000 to 20000 iterations to converge, so I need to accelerate the estimation of the wall temperature along the z axis.

I am looking for suggestions to get the coupling done faster. I guess there must be a better approach than mine, as the integration part takes far longer than the 3D simulation.

Initially I was thinking to split the boundaries into smaller chunks and not using a condition when integrating, but that won't help as you can see in the time comparison of different integrations at the bottom of the source code.

I am running Mathematica 12.1.

Full code:

Needs["NDSolve`FEM`"];(*constants*)
Lp = 0.25;
da = 0.02;
hi = 0.15;
ha = 0.15;
ks = 2.1;
alphaf = 1000;
alphai = 6;
alphaa = 0.6;
ra = da/2;
Hi = hi + ra;
Ha = ha + ra;
H = Hi + Ha;
cW = 4200;
rhoW = 1000;
kW = 0.6;
l = 1;
(*Vf=10 Lp l/3600000;*)
Vf = 3.14159*10^-5;(*volume flux water for Reynolds number=2000*)

mpkt = VfrhoW;
deltaT = 5; (doubled by symmetry, channel simulation using whole 

diameter while calculating only symmetry half)
Qges = mpktdeltaTcW (required heat to heat the fluid*)


areaHeat = H*l;


qzu = Qges/areaHeat(heat flux density required on boundary)


(mesh)
pointsStructure = {{0, 0}, {Lp/2, 0}, {Lp/2, H}, {0, H}};
(pointsPipeOuter=Table[ra {Cos[theta Degree],Sin[theta 

Degree]}+{0,Ha},{theta,90,-90,-20}];)
pointsPipeOuter = 
  Table[ra {Cos[theta Degree], Sin[theta Degree]} + {0, Ha}, {theta, 
    90, -90, -20}];
{len1, len2} = Length /@ {pointsStructure, pointsPipeOuter};
contour = 
  Table[{i, If[i == len1 + len2, 1, i + 1]}, {i, 1, len1 + len2}];
line1D = MeshRegion[Table[{i}, {i, 0, l, l/50.}], 
   Line /@ Table[{i, i + 1}, {i, 50}]];
bmesh = ToBoundaryMesh[
   "Coordinates" -> Join[pointsStructure, pointsPipeOuter], 
   "BoundaryElements" -> {LineElement[contour]}];
mesh2D = ToElementMesh[bmesh, "MeshOrder" -> 1, 
   MaxCellMeasure -> 10^-4];


(*
Print["mesh2D"]
mesh2D["Wireframe"]
Print["region2D"]
*)


region2D = 
  MeshRegion[mesh2D["Coordinates"], 
   Triangle /@ mesh2D["MeshElements"][[1, 1]]];


(Print["region3D"])
region3D = RegionProduct[region2D, line1D];
(Print["mesh3D"])
mesh3D = ToElementMesh[region3D(*,MaxCellMeasure[Rule]0.05 10^-5*)]


(Print["mesh3D styled"]
groups=mesh3D["BoundaryElementMarkerUnion"];
temp=Most[Range[0,1,1/(Length[groups])]];
colors=ColorData["BrightBands"][#]&/@temp;
mesh3D["Wireframe"["MeshElementStyle"[Rule]FaceForm/@colors,

ViewPoint[Rule]{0.5,-1.5,0.5}]]
)


(Inspect element markers)
bmesh = ToBoundaryMesh[mesh3D]


groups = mesh3D["BoundaryElementMarkerUnion"];
temp = Most[Range[0, 1, 1/(Length[groups])]];
colors = ColorData["BrightBands"][#] & /@ temp;


surfaces = 
  AssociationThread[groups, 
   bmesh["Wireframe"[ElementMarker == #, 
       "MeshElementStyle" -> FaceForm[colors[[#]]]]] & /@ groups];
Manipulate[
 Show[{bmesh["Edgeframe"], choices /. surfaces}], {{choices, groups}, 
  groups, CheckboxBar}, ControlPlacement -> Top]


(3,4,6,7,9,10,11,12,13)(Channel)
(1,2,5,8,14,15,16)(notChannel)
(15)(back side for heat flux)


(###Calculate surface from geometry###)


(Plotting lines used for geometry)
Print["Plotting lines used for geometry"];
plotGeometryLines = ListLinePlot[pointsPipeOuter,
  PlotStyle -> {Thick, Orange},
  AspectRatio -> Automatic]


Print["Circumference of channel (geometry):"];
circumferenceNumeric = 2Plus @@
   Table[EuclideanDistance[pointsPipeOuter[[i]], 
     pointsPipeOuter[[i + 1]]]
    , {i, Length[pointsPipeOuter] - 1}
    ]
Print["Circumference of channel(analytic definition):"];
circumferenceAnalyt = Pi  da


Print["Diameter by circumference of channel:"];
dNumericCirc = circumferenceNumeric/Pi
Print["Diameter of channel(analytic definition):"];
da


(Setting diamaeter for calculation,
matching surface of channel calculation with channel surface of the 

solid)
diamaterEff = dNumericCirc;


(1d mesh for channel simulation)
numElements = 150;
lst1coordinates = Table[{i}, {i, 0, l, l/numElements}];
lst2lines = Table[{i, i + 1}, {i, 1, Length[lst1coordinates] - 1}];


mesh1DFlow = 
 ToElementMesh["Coordinates" -> lst1coordinates, 
  "MeshElements" -> {LineElement[lst2lines]}]


(stuff of forum post approach, not used anymore)
(###### useless start #######)
numLines = 9;
x0 = 0;
y0 = 0.16;


xyListBereiche = Table[
   {Sin[Pi/numLines*(i)]ra + x0,(x-coord)
    Cos[Pi/numLines(i)]ra + y0(y-coord)}
   , {i, 0, numLines, 1}];
xyListLinePos = Table[
   {Sin[Pi/numLines(i + 0.5)]ra + x0,(x-coord)
    Cos[Pi/numLines(i + 0.5)]ra + y0(y-coord*)}
   , {i, 0, numLines - 1, 1}];


xyListSurface = {};
Do[
 xSur = (xyListBereiche[[i, 1]] + xyListBereiche[[i + 1, 1]])/2;
 ySur = (xyListBereiche[[i, 2]] + xyListBereiche[[i + 1, 2]])/2;


AppendTo[xyListSurface, {xSur, ySur}];


, {i, Length[xyListBereiche] - 1}]


plotPoints = 
  ListPlot[{xyListLinePos, xyListBereiche, xyListSurface}, 
   AspectRatio -> Automatic,
   BaseStyle -> PointSize[0.03(.035)],
   PlotStyle -> {Blue, Red, Green},
   AxesOrigin -> {x0, y0}
   ];


Show[
 {plotPoints, plotGeometryLines}
 , PlotRange -> All]


(*
Solution from forum post only using line at x=0,y=0.15 (bottom red 

dot);
blue dots too far from boundary, TwNeu;
red dots for lines on edges, TwNeu2;
green dots in the middle of the boundary pieces, TwNeu3;
)
(###### useless end #######*)


(calculate initial values)
eq = {-Inactive[
       Div][{{-ks, 0, 0}, {0, -ks, 0}, {0, 0, -ks}}.Inactive[Grad][
        t[x, y, z], {x, y, z}], {x, y, z}]
    ==(NeumannValue[alphai t[x,y,z],y[Equal]H]
    +NeumannValue[alphaa t[x,y,z],y[Equal]0])
    NeumannValue[-qzu, ElementMarker == 15]
     + NeumannValue[alphaf (t[x, y, z] - tf[x, y, z]), 
      ElementMarker == 3 || ElementMarker == 4 || ElementMarker == 6 ||
        ElementMarker == 7 || ElementMarker == 9 || 
       ElementMarker == 10 || ElementMarker == 11 || 
       ElementMarker == 12 || ElementMarker == 13(x^2+(y-
      Ha)^2[Equal]ra^2)],
   -cW rhoW Vf D[tf[x, y, z], z] == 
    Pi diamaterEff alphaf (tf[x, y, z] - t[x, y, z]), 
   DirichletCondition[tf[x, y, z] == 10, z == 0]};
{T, Tf} = NDSolveValue[eq, {t, tf}, Element[{x, y, z}, mesh3D]];


(Calculation stuff)
Tn[0][x_, y_, z_] := 
 T[x, y, z] (List/function of solid temperatures of different 

iterations)
Tfn[0][z_] := 
 T[0, Ha - ra, 
  z] (List/function of channel temperatures of different iterations)


TEnd = {};(Outlet Temperature list over iterations)
AppendTo[TEnd, Tfn[0][l]];


(keep track of timing, lists filled while iterating)
timesChan = {};
timesSol = {};
timesAll = {};
timesIntegrate = {};


(###### useless start #######)
Tw[i_, z_] := Tn[i][0, Ha - ra, z];


TwNeu[i_, z_] := (1/numLines)Plus @@
    Table[
     (Print["xy: "<>ToString[xy]<>" Tn[i]["<>ToString[xy]<>","<>
     ToString[z]<>"]: "<>ToString[Tn[i][First@xy,Last@xy,z]]];*)
     Tn[i][First@xy, Last@xy, z]
     , {xy, xyListLinePos}];


TwNeu2[i_, z_] := (1/(numLines + 1))Plus @@
    Table[
     (Print["xy: "<>ToString[xy]<>" Tn[i]["<>ToString[xy]<>","<>
     ToString[z]<>"]: "<>ToString[Tn[i][First@xy,Last@xy,z]]];*)
     Tn[i][First@xy, Last@xy, z]
     , {xy, xyListBereiche}];


TwNeu3[i_, z_] := (1/(numLines))Plus @@
    Table[
     (Print["TwNeu3, z: "<>ToString[z]];)
     (Print["xy: "<>ToString[xy]<>" Tn[i]["<>ToString[xy]<>","<>
     ToString[z]<>"]: "<>ToString[Tn[i][First@xy,Last@xy,z]]];)
     Tn[i][First@xy, Last@xy, z]
     , {xy, xyListSurface}];
(###### useless end #######*)


(Integration stuff)
chanPart[x_, y_, z_][zmin_, zmax_] := 
 zmin <= z <= zmax; (condition for partial integration over boundary)


numPieces = 20(numElements);


deltaZ = l/numPieces;


(z coordinates for interpolation function with average temperature 

integration)
tempZs = Table[
   (i + 0.5)*deltaZ
   , {i, 0, numPieces - 1}
   ];
PrependTo[tempZs, 0];
AppendTo[tempZs, l];


(area of integration pieces for averaging temperature)
areaPiece = 
  FEMNBoundaryIntegrate[1, {x, y, z}, bmesh, 
    ElementMarker == 3 || ElementMarker == 4 || ElementMarker == 6 || 
     ElementMarker == 7 || ElementMarker == 9 || ElementMarker == 10 ||
      ElementMarker == 11 || ElementMarker == 12 || 
     ElementMarker == 13]/numPieces;


relLenEndPiece = 
 1/200;(relative length of integration pieces for ends of 

interpolating function of wall temperature)
areaFrontBackPiece = areaPiece * numPieces*relLenEndPiece;


n = 8;(number of iterations)


(##### Main loop ######)
Do[
 Print["Iteration: " <> ToString[i]];


allTime = Timing[


(##### solve solid ######)
   time1 = Timing[
     Tn[i] = NDSolveValue[
       {-Inactive[
            Div][{{-ks, 0, 0}, {0, -ks, 0}, {0, 0, -ks}}.Inactive[
              Grad][t[x, y, z], {x, y, z}], {x, y, z}]
         ==(NeumannValue[alphai t[x,y,z],y[Equal]H]
         +NeumannValue[alphaa t[x,y,z],y[Equal]0])
         NeumannValue[-qzu, ElementMarker == 15]
          + 
          NeumannValue[alphaf (t[x, y, z] - Tfn[i - 1][z]), 
           ElementMarker == 3 || ElementMarker == 4 || 
            ElementMarker == 6 || ElementMarker == 7 || 
            ElementMarker == 9 || ElementMarker == 10 || 
            ElementMarker == 11 || ElementMarker == 12 || 
            ElementMarker == 13(x^2+(y-Ha)^2[Equal]ra^2)]},
       t, Element[{x, y, z}, mesh3D],
       Method -> {"PDEDiscretization" -> {"FiniteElement", 
           "InterpolationOrder" -> {T -> 2}}}
       ];(End NDSolve solid)
     ];(End timing NDSolve slid)


(##### Integration wall temperature function ####)
   integrateTime = First@Timing[


  (*partially integrate channel surface*)
  temps = Table[
    FEMNBoundaryIntegrate[
      Piecewise[{{Tn[i][x, y, z], 
         chanPart[x, y, z][num*deltaZ, (num + 1)*deltaZ]}, {0, 
         True}}],
      {x, y, z}, bmesh, 
      ElementMarker == 3 || ElementMarker == 4 || 
       ElementMarker == 6 || ElementMarker == 7 || 
       ElementMarker == 9 || ElementMarker == 10 || 
       ElementMarker == 11 || ElementMarker == 12 || 
       ElementMarker == 13]/areaPiece
    , {num, 0, numPieces - 1}];

  (*add values for z=0 and z=l*)
  PrependTo[temps,
   FEMNBoundaryIntegrate[
     Piecewise[{{Tn[i][x, y, z], 
        chanPart[x, y, z][0, l*relLenEndPiece]}, {0, True}}],
     {x, y, z}, bmesh, 
     ElementMarker == 3 || ElementMarker == 4 || 
      ElementMarker == 6 || ElementMarker == 7 || 
      ElementMarker == 9 || ElementMarker == 10 || 
      ElementMarker == 11 || ElementMarker == 12 || 
      ElementMarker == 13]/areaFrontBackPiece
   ];
  AppendTo[temps,
   FEMNBoundaryIntegrate[
     Piecewise[{{Tn[i][x, y, z], 
        chanPart[x, y, z][l*(1 - 1*relLenEndPiece), l]}, {0, 
        True}}],
     {x, y, z}, bmesh, 
     ElementMarker == 3 || ElementMarker == 4 || 
      ElementMarker == 6 || ElementMarker == 7 || 
      ElementMarker == 9 || ElementMarker == 10 || 
      ElementMarker == 11 || ElementMarker == 12 || 
      ElementMarker == 13]/areaFrontBackPiece
   ];

  (*associate average temperature values to z coordinates*)
  tempPointsZ = Transpose[{tempZs, temps}];

  (*create actual wall temperature function*)
  tempIntegrateInterpFun = 
   Interpolation[tempPointsZ, InterpolationOrder -&gt; 2];
  ];(*End Timing Integration*)




AppendTo[timesIntegrate, integrateTime];


Print["Integrate T[z=0.5l]: " <> 
     ToString[tempIntegrateInterpFun[0.5]](<>"TwNeu: "<>ToString[
    TwNeu[i,0.5l]]<>", TwNeu2: " <> ToString[TwNeu2[i,0.5l]]<>
    ", TwNeu3: " <> ToString[TwNeu3[i,0.5l]]<>", TWAlt: " <> ToString[
    Tw[i,0.5l]])];


(##### Solve channel ######)
   time2 = Timing[
     Tfn[i] = NDSolveValue[
       {-cW rhoW Vf D[tf[z], z]
         == 
         Pi diamaterEff alphaf (tf[z] - 
            tempIntegrateInterpFunz),
        tf[0] == 10},
       tf, {z} [Element] mesh1DFlow
       (,Method[Rule]{SpatialDiscretization[Rule]{FiniteElement,
       MeshOptions[Rule]MaxCellMeasure[Rule]0.01}})
       ];(End NDSolve channel)


 AppendTo[TEnd, Tfn[i][l]];
 ];(*End Timing solve channel*)



AppendTo[timesChan, First@time2];
   AppendTo[timesSol, First@time1];
   ]; (allTime)
 AppendTo[timesAll, First@allTime];
 , {i, 1, n}
 ](End Do Loop)


(Plotting values)
Plot[Evaluate[Table[Tfn[i][z], {i, 1, n, 1}]], {z, 0, l},
 BaseStyle -> {Thin(,Black)},
 PlotLegends -> Table["It " <> ToString@i, {i, 1, n, 1}],
 PlotLabel -> "Channel temperature over z for iterations"]


ListPlot[TEnd,
 PlotLabel -> "Outlet temperature channel over iterations"]


plotTempPointsZ = 
  ListPlot[tempPointsZ, 
   PlotLegends -> {"tempPointsZ from integration"}];
plotTempIntegrateInterpFun = 
  Plot[tempIntegrateInterpFun[z], {z, 0., l}, 
   PlotLegends -> {"tempIntegrateInterpFun"}];
Show[{plotTempPointsZ, plotTempIntegrateInterpFun},
 PlotLabel -> "Integration wall temperature"
 , PlotRange -> All]


ListPlot[{timesAll, timesIntegrate, timesSol, timesChan},
 PlotLegends -> {"All", "Integration", "Solid", "Channel"},
 PlotLabel -> "Timings"]


Table[ContourPlot[Tn[i][x, y, .5 l], {x, 0, .125}, {y, 0, .32}, 
  ColorFunction -> Hue, Contours -> 20, PlotLegends -> Automatic, 
  AspectRatio -> Automatic, ImageSize -> Medium, 
  PlotLabel -> "Iteration " <> ToString@i], {i, 1, n, 2}]


Show[
 {
  plotTempPointsZ,
  Plot[{Tw[n, z], TwNeu[n, z], TwNeu2[n, z], TwNeu3[n, z], 
    tempIntegrateInterpFun[z]}, {z, 0, l},
   PlotStyle -> {Red, Green, Blue, Orange}, 
   PlotLegends -> {"TwAlt", "TwNeu", "TwNeu2", "TwNeu3", 
     "tempIntegrateInterpFun"}, BaseStyle -> {Thick}]
  },
 ImageSize -> 750
 , PlotRange -> All]


(Energy balance analysis)
(Pipe stuff)
mpkt = Vf*rhoW;
Tin = Tfn[n][0];
Tout = Tfn[n][l];


QchannelOrg = mpktcW(Tout - Tin);
Qchannel = QchannelOrg/2;(symmetry)


(Wall stuff)
Qwall = FEMNBoundaryIntegrate[
   ks*Derivative[1, 0, 0][Tn[n]][x, y, z], {x, y, z}, bmesh, 
   ElementMarker == 15];


deltaQ = Qchannel - Qwall;
QerrorRel = deltaQ/Qwall;


(Output)
Print["Tin: " <> ToString[Tin] <> ", Tout: " <> ToString[Tout] <> 
  ", Qchannel: " <> ToString[Qchannel] <> ", Qwall: " <> 
  ToString[Qwall] <> ", deltaQ: " <> ToString[deltaQ] <> 
  ", QerrorRel: " <> ToString[QerrorRel*100] <> "%" <> 
  ", Mean time Iteration: " <> ToString[Mean[timesAll]] <> 
  ", Mean time Integration: " <> ToString[Mean[timesIntegrate]] <> 
  ", Iterations: " <> ToString[n] <> ", 1D elements: " <> 
  ToString[numElements] <> ", Integration elements: " <> 
  ToString[numPieces]
 ]


(example output;

"Tin: 10., Tout: 20., Qchannel: 659.737, Qwall: 659.733, deltaQ: 

0.0042714, QerrorRel: 0.000647444%, Mean time Iteration: 14.2031, 

Mean time Integration: 12.2879, Iterations: 7, 1D elements: 150, 

Integration elements: 20"
)


(Testing integration time)


Print["### Integrating over whole channel ###"];
timeTest = Timing[
   val = FEMNBoundaryIntegrate[1, {x, y, z}, bmesh, 
     ElementMarker == 3 || ElementMarker == 4 || ElementMarker == 6 ||
       ElementMarker == 7 || ElementMarker == 9 || 
      ElementMarker == 10 || ElementMarker == 11 || 
      ElementMarker == 12 || ElementMarker == 13]
   ];
Print["channel area time: " <> ToString@First@timeTest <> 
   ", Value: " <> ToString@val];


timeTest = Timing[
   elementNumber = {3, 4, 6, 7, 9, 10, 11, 12, 13};
   tsIndividual = {};
   val = Plus @@ Table[
      AppendTo[tsIndividual, First@Timing[
         areaIndi = 
           FEMNBoundaryIntegrate[1, {x, y, z}, bmesh, 
            ElementMarker == i];
         ]
       ];
      areaIndi
      , {i, elementNumber}
      ];
   ];
Print["channel area individual element marker integration time: " <> 
  ToString@First@timeTest <> ", Value: " <> ToString@val <> 
  ", times: " <> 
  ToString@tsIndividual](<>", sum of individual integration times: 

"<>ToString@Plus@@tsIndividual];)


timeTest = Timing[
   val = FEMNBoundaryIntegrate[Tn[n][x, y, z], {x, y, z}, bmesh, 
     ElementMarker == 3 || ElementMarker == 4 || ElementMarker == 6 ||
       ElementMarker == 7 || ElementMarker == 9 || 
      ElementMarker == 10 || ElementMarker == 11 || 
      ElementMarker == 12 || ElementMarker == 13]
   ];
Print["channel temp time: " <> ToString@First@timeTest <> 
   ", Value: " <> ToString@val];


Print[""];
Print["### Integrating piecewise over whole channel ###"];


numPiecesTEST = 10(numElements);


deltaZTEST = l/numPiecesTEST;


timeTest = Timing[
   tsIndividual = {};
   valList = Table[
     timePieceTest = First@Timing[
        tempPieceTest = 
         FEMNBoundaryIntegrate[
          Piecewise[{{1, 
             chanPart[x, y, z][
              numdeltaZTEST, (num + 1)deltaZTEST]}, {0, True}}],
          {x, y, z}, bmesh, 
          ElementMarker == 3 || ElementMarker == 4 || 
           ElementMarker == 6 || ElementMarker == 7 || 
           ElementMarker == 9 || ElementMarker == 10 || 
           ElementMarker == 11 || ElementMarker == 12 || 
           ElementMarker == 13]
        ];
     AppendTo[tsIndividual, timePieceTest];
     tempPieceTest
     , {num, 0, numPiecesTEST - 1}];
   ];
Print["channel piecewise area time: " <> ToString@First@timeTest <> 
   ", Value: " <> ToString[Plus @@ valList] <> ", times: " <> 
   ToString@tsIndividual];


timeTest = Timing[
   tsIndividual = {};
   valList = Table[
     timePieceTest = First@Timing[
        tempPieceTest = 
         FEMNBoundaryIntegrate[
          Piecewise[{{Tn[n][x, y, z], 
             chanPart[x, y, z][
              numdeltaZTEST, (num + 1)deltaZTEST]}, {0, True}}],
          {x, y, z}, bmesh, 
          ElementMarker == 3 || ElementMarker == 4 || 
           ElementMarker == 6 || ElementMarker == 7 || 
           ElementMarker == 9 || ElementMarker == 10 || 
           ElementMarker == 11 || ElementMarker == 12 || 
           ElementMarker == 13]
        ];
     AppendTo[tsIndividual, timePieceTest];
     tempPieceTest
     , {num, 0, numPiecesTEST - 1}];
   ];
Print["channel piecewise temp time: " <> ToString@First@timeTest <> 
   ", Value: " <> ToString[Plus @@ valList] <> ", times: " <> 
   ToString@tsIndividual];


timeTest = Timing[
   val = FEMNBoundaryIntegrate[
     Piecewise[{{1, chanPart[x, y, z][0, l]}, {0, True}}],
     {x, y, z}, bmesh, 
     ElementMarker == 3 || ElementMarker == 4 || ElementMarker == 6 ||
       ElementMarker == 7 || ElementMarker == 9 || 
      ElementMarker == 10 || ElementMarker == 11 || 
      ElementMarker == 12 || ElementMarker == 13]
   ];
Print["whole channel with condition area time: " <> 
   ToString@First@timeTest <> ", Value: " <> ToString@val];


timeTest = Timing[
   val = FEMNBoundaryIntegrate[
     Piecewise[{{Tn[n][x, y, z], chanPart[x, y, z][0, l]}, {0, True}}],
     {x, y, z}, bmesh, 
     ElementMarker == 3 || ElementMarker == 4 || ElementMarker == 6 ||
       ElementMarker == 7 || ElementMarker == 9 || 
      ElementMarker == 10 || ElementMarker == 11 || 
      ElementMarker == 12 || ElementMarker == 13]
   ];
Print["whole channel with condition temp time: " <> 
   ToString@First@timeTest <> ", Value: " <> ToString@val];


Print[""];
Print["### Integrating over whole mesh ###"];


timeTest = Timing[
   val = FEMNBoundaryIntegrate[1, {x, y, z}, bmesh]
   ];
Print["whole mesh area time: " <> ToString@First@timeTest <> 
   ", Value: " <> ToString@val];


timeTest = Timing[
   val = FEMNBoundaryIntegrate[Tn[n][x, y, z], {x, y, z}, bmesh]
   ];
Print["whole mesh Temp time: " <> ToString@First@timeTest <> 
   ", Value: " <> ToString@val];


(*example output


"### Integrating over whole channel ###"
"channel area time: 0.234375, Value: 0.0312567"
"channel area individual element marker integration time: 1.20313, 

Value: 0.0312567, times: {0.109375, 0.140625, 0.140625, 0.140625, 

0.125, 0.125, 0.140625, 0.140625, 0.140625}"
"channel temp time: 0.734375, Value: 1.12885"


"### Integrating piecewise over whole channel ###"
"channel piecewise area time: 2.32813, Value: 0.0312567, times: 

{0.265625, 0.21875, 0.265625, 0.21875, 0.203125, 0.1875, 0.265625, 

0.21875, 0.21875, 0.265625}"
"channel piecewise temp time: 5.64063, Value: 1.12885, times: 

{0.5625, 0.546875, 0.578125, 0.609375, 0.53125, 0.609375, 0.5, 

0.546875, 0.578125, 0.578125}"
"whole channel with condition area time: 0.234375, Value: 0.0312567"
"whole channel with condition temp time: 0.609375, Value: 1.12885"


"### Integrating over whole mesh ###"
"whole mesh area time: 0.296875, Value: 0.980949"
"whole mesh Temp time: 1.0625, Value: 265.323"


*)
Tobias
  • 563
  • 2
  • 7
  • This is quite a lot of code and text. Here are some suggestions to improve your question: Start by saying (in equations) what you actually want to compute. Then show the best approach that you have so far and delete everything else. Try to simplify your issue. Right now it would take a considerable amount of time to understand what you are doing anything that helps to understand what you are up to would be a good improvement. – user21 Oct 01 '21 at 08:56
  • @Tobias Did you use method of false transient to solve your problem? – Alex Trounev Oct 01 '21 at 10:34
  • @AlexTrounev I did use the method of false transient as you proposed in your answer to the linked post. – Tobias Oct 01 '21 at 11:04
  • @user21 I will repost this question, narrowing down to my actual problem regarding the speedup of calculating the wall temperature as a function of the channel coordinate z. I will link this post for more information. – Tobias Oct 01 '21 at 11:04
  • @user21 I reposted the question and removed everything that is not necessary to run the code and not relevant for my coupling approach https://mathematica.stackexchange.com/questions/256355/fem-1d-3d-region-coupling-speed-up-coupling-using-boundary-integration – Tobias Oct 01 '21 at 16:03

0 Answers0