I am working on a simulation of the heat equation involving a 3D solid simulation coupled to a 1D fluid simulation (convective term of heat equation). I am using the method of false transient as proposed in this post.
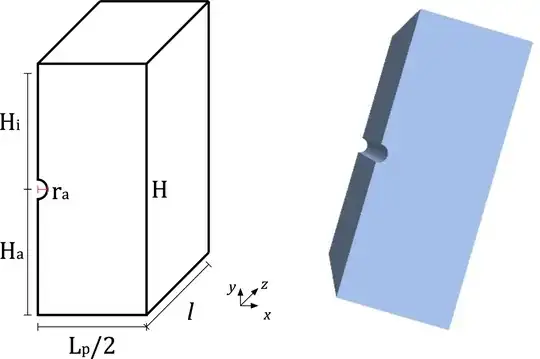
See the geometry below. The channel flow is in z-direction.
I am looking for suggestions how to speed up my method of coupling the regions.
This is a repost of my prior question, where my question was somewhat overloaded with irrelevant stuff.
The method of false transient works as follows:
Loop[
solve 3D solid with Neumann BC
(exchanging heat with the fluid based on fluid temperature as function of z)
calculate wall temperature (of the solid channel boundary) as function of z
solve 1D channel with Neumann BC
(exchanging heat with the solid based on wall temperature function of z)
]
In the post that proposed the method of the false transient, the wall temperature was estimated as the temperature along one line of the channel wall at a fixed x and y coordinate. But this approach did not ensure energy conservation, so I came up with an approach that does.
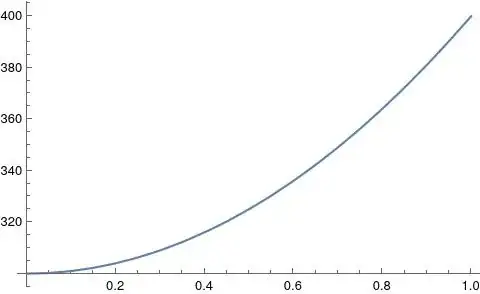
I am dividing the channel surface into a number of segments.(channel surface = cut out in the geometry above) Then I integrate the average temperature of each of those segments. Then I use those averaged temperatures to create an interpolation function of the average temperature as a function of the z-coordinate. The image below shows the average temperatures of the segments with the dots and the interpolatingfunction with the line. Note, that I added additional values for z=0 and z=l.
Before the Loop I am defining my integration coordinates and calculating the area of the segments:
(*Initialisation of integration stuff BEGIN*)
chanPart[x_, y_, z_][zmin_, zmax_] := zmin <= z <= zmax; (*condition for partial integration over boundary*)
numPieces = 20;
deltaZ = l/numPieces;
(z coordinates for interpolation function with average temperature
integration)
tempZs = Table[
(i + 0.5)*deltaZ
, {i, 0, numPieces - 1}
];
PrependTo[tempZs, 0];
AppendTo[tempZs, l];
(area of integration pieces for averaging temperature)
areaPiece =
FEMNBoundaryIntegrate[1, {x, y, z}, bmesh,
ElementMarker == 3 || ElementMarker == 4 || ElementMarker == 6 ||
ElementMarker == 7 || ElementMarker == 9 || ElementMarker == 10 ||
ElementMarker == 11 || ElementMarker == 12 ||
ElementMarker == 13]/numPieces;
relLenEndPiece =
1/200;(relative length of integration pieces for ends of
interpolating function of wall temperature)
areaFrontBackPiece = areaPiece * numPiecesrelLenEndPiece;
(Initialisation of integration stuff END*)
In the simulation loop I am integrating the segments and create the interpolation function:
(*##### Integration wall temperature function BEGIN####*)
integrateTime = First@Timing[
(partially integrate channel surface)
temps = Table[
FEMNBoundaryIntegrate[
Piecewise[{{Tn[i][x, y, z],
chanPart[x, y, z][numdeltaZ, (num + 1)deltaZ]}, {0,
True}}],
{x, y, z}, bmesh,
ElementMarker == 3 || ElementMarker == 4 ||
ElementMarker == 6 || ElementMarker == 7 ||
ElementMarker == 9 || ElementMarker == 10 ||
ElementMarker == 11 || ElementMarker == 12 ||
ElementMarker == 13]/areaPiece
, {num, 0, numPieces - 1}];
(add values for z=0 and z=l)
PrependTo[temps,
FEMNBoundaryIntegrate[
Piecewise[{{Tn[i][x, y, z],
chanPart[x, y, z][0, l*relLenEndPiece]}, {0, True}}],
{x, y, z}, bmesh,
ElementMarker == 3 || ElementMarker == 4 || ElementMarker == 6 ||
ElementMarker == 7 || ElementMarker == 9 ||
ElementMarker == 10 || ElementMarker == 11 ||
ElementMarker == 12 || ElementMarker == 13]/areaFrontBackPiece
];
AppendTo[temps,
FEMNBoundaryIntegrate[
Piecewise[{{Tn[i][x, y, z],
chanPart[x, y, z][l(1 - 1relLenEndPiece), l]}, {0, True}}],
{x, y, z}, bmesh,
ElementMarker == 3 || ElementMarker == 4 || ElementMarker == 6 ||
ElementMarker == 7 || ElementMarker == 9 ||
ElementMarker == 10 || ElementMarker == 11 ||
ElementMarker == 12 || ElementMarker == 13]/areaFrontBackPiece
];
(associate average temperature values to z coordinates)
tempPointsZ = Transpose[{tempZs, temps}];
(create actual wall temperature function)
tempIntegrateInterpFun =
Interpolation[tempPointsZ, InterpolationOrder -> 2];
];(End Timing Integration)
(##### Integration wall temperature function END####)
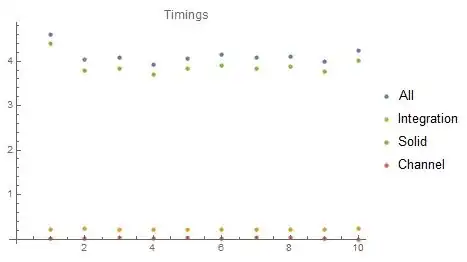
This approach works surprisingly well and I am getting an energy conservation error in the order of 10^-6 (relative to incoming heat flux into the solid). But it is pretty slow. The integration takes up most of the time per iteration. See the timing over the iterations below.
I want to use this approach with simulations that take about 5000 to 20000 iterations to converge, so I need to speed this up. Could I somehow extract some information from the mesh prior to the loop to access the interpolatingfunction of the 3D solution of the solid directly in the loop and save time by not actually calling the NIntegrate function? Or perhaps there even is a way simpler method available in Mathematica to estimate my wall temperature as a function of z?
Find my whole code below. It is quite long, but I structured it into blocks. The interesting part is in the block "Actual calculation". There you can find the two code segments discussed above about my integration approach.
Needs["NDSolve`FEM`"];
(*constants BEGIN*)
Lp = 0.25; da = 0.02; hi = 0.15; ha = 0.15;
ks = 2.1; alphaf = 1000; alphai = 6; alphaa = 0.6;
ra = da/2; Hi = hi + ra; Ha = ha + ra; H = Hi + Ha;
cW = 4200; rhoW = 1000; kW = 0.6;
l = 1;
Vf = 3.1415910^-5;(volume flux water for Reynolds number=2000*)
mpkt = VfrhoW;(Mass flow)
deltaT = 5; (doubled by symmetry, channel simulation using whole
diameter while calculating only symmetry half)
Qges = mpktdeltaTcW ;(required heat to heat the fluid*)
areaHeat = H*l;
qzu = Qges/areaHeat;(heat flux density required on boundary)
(constants END)
(Meshing BEGIN)
pointsStructure = {{0, 0}, {Lp/2, 0}, {Lp/2, H}, {0, H}};
pointsPipeOuter =
Table[ra {Cos[theta Degree], Sin[theta Degree]} + {0, Ha}, {theta,
90, -90, -20}];
{len1, len2} = Length /@ {pointsStructure, pointsPipeOuter};
contour =
Table[{i, If[i == len1 + len2, 1, i + 1]}, {i, 1, len1 + len2}];
line1D = MeshRegion[Table[{i}, {i, 0, l, l/50.}],
Line /@ Table[{i, i + 1}, {i, 50}]];
bmesh = ToBoundaryMesh[
"Coordinates" -> Join[pointsStructure, pointsPipeOuter],
"BoundaryElements" -> {LineElement[contour]}];
mesh2D = ToElementMesh[bmesh, "MeshOrder" -> 1,
MaxCellMeasure -> 10^-4];
region2D =
MeshRegion[mesh2D["Coordinates"],
Triangle /@ mesh2D["MeshElements"][[1, 1]]];
region3D = RegionProduct[region2D, line1D];
mesh3D = ToElementMesh[region3D]
(Meshing END)
(Inspect element markers BEGIN)
bmesh = ToBoundaryMesh[mesh3D]
groups = mesh3D["BoundaryElementMarkerUnion"];
temp = Most[Range[0, 1, 1/(Length[groups])]];
colors = ColorData["BrightBands"][#] & /@ temp;
surfaces =
AssociationThread[groups,
bmesh["Wireframe"[ElementMarker == #,
"MeshElementStyle" -> FaceForm[colors[[#]]]]] & /@ groups];
Manipulate[
Show[{bmesh["Edgeframe"], choices /. surfaces}], {{choices, groups},
groups, CheckboxBar}, ControlPlacement -> Top]
(3,4,6,7,9,10,11,12,13)(Channel)
(1,2,5,8,14,15,16)(notChannel)
(15)(back side for heat flux)
(Inspect element markers END)
(###Calculate effective diameter BEGIN###)
(channel surface of geometry is smaller than round cylinder due to
discretization)
circumferenceNumeric = 2Plus @@
Table[EuclideanDistance[pointsPipeOuter[[i]],
pointsPipeOuter[[i + 1]]]
, {i, Length[pointsPipeOuter] - 1}
];(calculating circumference of discretized channel)
dNumericCirc = circumferenceNumeric/Pi;
diamaterEff =
dNumericCirc;(Setting diamaeter for calculation, matching surface
of channel calculation with channel surface of the solid)
(###Calculate effective diameter END###*)
(1d mesh for channel simulation BEGIN)
numElements = 150;
lst1coordinates = Table[{i}, {i, 0, l, l/numElements}];
lst2lines = Table[{i, i + 1}, {i, 1, Length[lst1coordinates] - 1}];
mesh1DFlow =
ToElementMesh["Coordinates" -> lst1coordinates,
"MeshElements" -> {LineElement[lst2lines]}]
(1d mesh for channel simulation END)
(calculate starting values for main loop BEGIN)
eq = {-Inactive[
Div][{{-ks, 0, 0}, {0, -ks, 0}, {0, 0, -ks}}.Inactive[Grad][
t[x, y, z], {x, y, z}], {x, y, z}]
==(NeumannValue[alphai t[x,y,z],y[Equal]H]
+NeumannValue[alphaa t[x,y,z],y[Equal]0])
NeumannValue[-qzu, ElementMarker == 15]
+ NeumannValue[alphaf (t[x, y, z] - tf[x, y, z]),
ElementMarker == 3 || ElementMarker == 4 || ElementMarker == 6 ||
ElementMarker == 7 || ElementMarker == 9 ||
ElementMarker == 10 || ElementMarker == 11 ||
ElementMarker == 12 || ElementMarker == 13(x^2+(y-
Ha)^2[Equal]ra^2)],
-cW rhoW Vf D[tf[x, y, z], z] ==
Pi diamaterEff alphaf (tf[x, y, z] - t[x, y, z]),
DirichletCondition[tf[x, y, z] == 10, z == 0]};
{T, Tf} = NDSolveValue[eq, {t, tf}, Element[{x, y, z}, mesh3D]];
(calculate starting values for main loop END)
(###### Actual calculation BEGIN #########)
Tn[0][x_, y_, z_] :=
T[x, y, z] (List/function of solid temperatures of different
iterations)
Tfn[0][z_] :=
T[0, Ha - ra,
z] (List/function of channel temperatures of different iterations)
TEnd = {Tfn[0][l]};(Outlet Temperature list over iterations)
(keep track of timing, lists filled while iterating)
timesChan = {};
timesSol = {};
timesAll = {};
timesIntegrate = {};
(Initialisation of integration stuff BEGIN)
chanPart[x_, y_, z_][zmin_, zmax_] :=
zmin <= z <= zmax; (condition for partial integration over boundary)
numPieces = 20;
deltaZ = l/numPieces;
(z coordinates for interpolation function with average temperature
integration)
tempZs = Table[
(i + 0.5)*deltaZ
, {i, 0, numPieces - 1}
];
PrependTo[tempZs, 0];
AppendTo[tempZs, l];
(area of integration pieces for averaging temperature)
areaPiece =
FEMNBoundaryIntegrate[1, {x, y, z}, bmesh,
ElementMarker == 3 || ElementMarker == 4 || ElementMarker == 6 ||
ElementMarker == 7 || ElementMarker == 9 || ElementMarker == 10 ||
ElementMarker == 11 || ElementMarker == 12 ||
ElementMarker == 13]/numPieces;
relLenEndPiece =
1/200;(relative length of integration pieces for ends of
interpolating function of wall temperature)
areaFrontBackPiece = areaPiece * numPiecesrelLenEndPiece;
(Initialisation of integration stuff END*)
n = 8;(number of iterations)
(##### Main loop BEGIN######)
Do[
Print["Iteration: " <> ToString[i]];
allTime = Timing[
(##### solve solid ######)
time1 = Timing[
Tn[i] = NDSolveValue[
{-Inactive[
Div][{{-ks, 0, 0}, {0, -ks, 0}, {0, 0, -ks}}.Inactive[
Grad][t[x, y, z], {x, y, z}], {x, y, z}]
== NeumannValue[-qzu, ElementMarker == 15]
+
NeumannValue[alphaf (t[x, y, z] - Tfn[i - 1][z]),
ElementMarker == 3 || ElementMarker == 4 ||
ElementMarker == 6 || ElementMarker == 7 ||
ElementMarker == 9 || ElementMarker == 10 ||
ElementMarker == 11 || ElementMarker == 12 ||
ElementMarker == 13]},
t, Element[{x, y, z}, mesh3D],
Method -> {"PDEDiscretization" -> {"FiniteElement",
"InterpolationOrder" -> {T -> 2}}}
];(*End NDSolve solid*)
];(*End timing NDSolve slid*)
(##### Integration wall temperature function BEGIN####)
integrateTime = First@Timing[
(*partially integrate channel surface*)
temps = Table[
FEMNBoundaryIntegrate[
Piecewise[{{Tn[i][x, y, z],
chanPart[x, y, z][num*deltaZ, (num + 1)*deltaZ]}, {0,
True}}],
{x, y, z}, bmesh,
ElementMarker == 3 || ElementMarker == 4 ||
ElementMarker == 6 || ElementMarker == 7 ||
ElementMarker == 9 || ElementMarker == 10 ||
ElementMarker == 11 || ElementMarker == 12 ||
ElementMarker == 13]/areaPiece
, {num, 0, numPieces - 1}];
(*add values for z=0 and z=l*)
PrependTo[temps,
FEMNBoundaryIntegrate[
Piecewise[{{Tn[i][x, y, z],
chanPart[x, y, z][0, l*relLenEndPiece]}, {0, True}}],
{x, y, z}, bmesh,
ElementMarker == 3 || ElementMarker == 4 ||
ElementMarker == 6 || ElementMarker == 7 ||
ElementMarker == 9 || ElementMarker == 10 ||
ElementMarker == 11 || ElementMarker == 12 ||
ElementMarker == 13]/areaFrontBackPiece
];
AppendTo[temps,
FEMNBoundaryIntegrate[
Piecewise[{{Tn[i][x, y, z],
chanPart[x, y, z][l*(1 - 1*relLenEndPiece), l]}, {0,
True}}],
{x, y, z}, bmesh,
ElementMarker == 3 || ElementMarker == 4 ||
ElementMarker == 6 || ElementMarker == 7 ||
ElementMarker == 9 || ElementMarker == 10 ||
ElementMarker == 11 || ElementMarker == 12 ||
ElementMarker == 13]/areaFrontBackPiece
];
(*associate average temperature values to z coordinates*)
tempPointsZ = Transpose[{tempZs, temps}];
(*create actual wall temperature function*)
tempIntegrateInterpFun =
Interpolation[tempPointsZ, InterpolationOrder -> 2];
];(*End Timing Integration*)
(##### Integration wall temperature function END####)
AppendTo[timesIntegrate, integrateTime];
Print["Integrate T[z=0.5*l]: " <>
ToString[tempIntegrateInterpFun[0.5]]];
(##### Solve channel ######)
time2 = Timing[
Tfn[i] = NDSolveValue[
{-cW rhoW Vf D[tf[z], z]
==
Pi diamaterEff alphaf (tf[z] -
tempIntegrateInterpFun[
z] (Heat flux boundary condition using the wall
temperature function)),
tf[0] == 10},
tf, {z} [Element] mesh1DFlow
];(End NDSolve channel)
AppendTo[TEnd, Tfn[i][l]];
];(*End Timing solve channel*)
AppendTo[timesChan, First@time2];
AppendTo[timesSol, First@time1];
]; (End timing iteration)
AppendTo[timesAll, First@allTime];
, {i, 1, n}
](##### Main loop END######)
(########## Actual calculation END ##########)
(Plotting results BEGIN)
Plot[Evaluate[Table[Tfn[i][z], {i, 1, n, 1}]], {z, 0, l},
BaseStyle -> {Thin(,Black)},
PlotLegends -> Table["It " <> ToString@i, {i, 1, n, 1}],
PlotLabel -> "Channel temperature over z for iterations"]
ListPlot[TEnd,
PlotLabel -> "Outlet temperature channel over iterations"]
plotTempPointsZ =
ListPlot[tempPointsZ,
PlotLegends -> {"tempPointsZ from integration"}];
plotTempIntegrateInterpFun =
Plot[tempIntegrateInterpFun[z], {z, 0., l},
PlotLegends -> {"tempIntegrateInterpFun"}];
Show[{plotTempPointsZ, plotTempIntegrateInterpFun},
PlotLabel -> "Integration wall temperature",
AxesLabel -> {"z", "Temperature"}
, PlotRange -> All]
ListPlot[{timesAll, timesIntegrate, timesSol, timesChan},
PlotLegends -> {"All", "Integration", "Solid", "Channel"},
PlotLabel -> "Timings"]
Table[ContourPlot[Tn[i][x, y, .5 l], {x, 0, .125}, {y, 0, .32},
ColorFunction -> Hue, Contours -> 20, PlotLegends -> Automatic,
AspectRatio -> Automatic, ImageSize -> Medium,
PlotLabel -> "Iteration " <> ToString@i], {i, 1, n, 2}]
(Plotting results END)
(Energy balance analysis BEGIN)
(Pipe stuff)
mpkt = Vf*rhoW;
Tin = Tfn[n][0];
Tout = Tfn[n][l];
QchannelOrg = mpktcW(Tout - Tin);
Qchannel = QchannelOrg/2;(symmetry)
(Wall stuff)
Qwall = FEMNBoundaryIntegrate[
ks*Derivative[1, 0, 0][Tn[n]][x, y, z], {x, y, z}, bmesh,
ElementMarker == 15];
deltaQ = Qchannel - Qwall;
QerrorRel = deltaQ/Qwall;
(Output)
Print["Tin: " <> ToString[Tin] <> ", Tout: " <> ToString[Tout] <>
", Qchannel: " <> ToString[Qchannel] <> ", Qwall: " <>
ToString[Qwall] <> ", deltaQ: " <> ToString[deltaQ] <>
", QerrorRel: " <> ToString[QerrorRel*100] <> "%" <>
", Mean time Iteration: " <> ToString[Mean[timesAll]] <>
", Mean time Integration: " <> ToString[Mean[timesIntegrate]] <>
", Iterations: " <> ToString[n] <> ", 1D elements: " <>
ToString[numElements] <> ", Integration elements: " <>
ToString[numPieces]
]
(Example output: Tin: 10., Tout: 20., Qchannel: 659.736, Qwall:
659.733, deltaQ: 0.00294866, QerrorRel: 0.000446948%, Mean time
Iteration: 13.4375, Mean time Integration: 11.6992, Iterations: 8, 1D
elements: 150, Integration elements: 20)
(Energy balance analysis END)



ExtrudeMeshfromMeshTools. Than in each slice $z_i$ average wall temperature is calculated by$T_w(z_i)=\int_{-\pi/2}^{\pi/2}T(r_a\cos\varphi,H_a+r_a\sin\varphi,z_i)d \varphi/\pi$. By avoiding surface integration we can diminish (I hope) calculation time – Oleksii Semenov Oct 11 '21 at 07:41