1

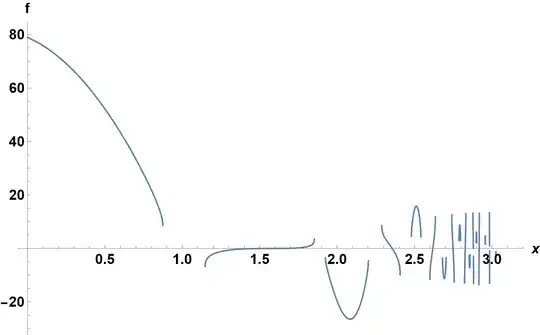
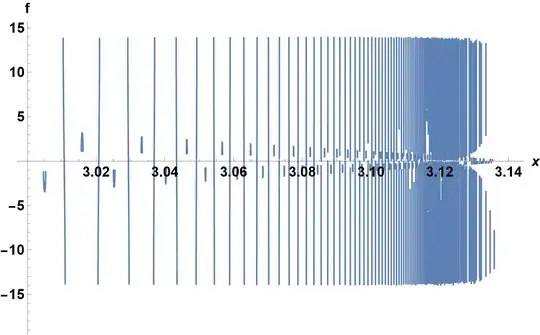
I have this function for reals $0<x<\pi$. $$f(x)=(3 \pi -2 x)^2 \sin \left(\frac{1}{2} \left(\csc ^{-1}\left(\frac{4 \pi (\pi -x) \csc \left(\frac{\pi ^2}{\pi -x}\right)}{4 x^2-8 \pi x+5 \pi ^2}\right)-\frac{\pi x}{\pi -x}+\pi \right)\right)\\-(\pi -2 x)^2 \sin \left(\frac{1}{2} \left(\csc ^{-1}\left(\frac{4 \pi (\pi -x) \csc \left(\frac{\pi ^2}{\pi -x}\right)}{4 x^2-8 \pi x+5 \pi ^2}\right)+\frac{\pi ^2}{\pi -x}\right)\right)$$

I try NSolve to obtain all the roots of the function over the domain, but, it seems that Mathematica needs much time to produce all the roots.

Is there any alternative for NSolve or Solve to obtain all the roots? Any comments are appreciated.

f = -(\[Pi] - 2 x)^2 Sin[ 1/2 (\[Pi]^2/(\[Pi] - x) +   ArcCsc[(4 \[Pi] (\[Pi] - x) Csc[\[Pi]^2/(\[Pi] - x)])/( 5 \[Pi]^2 - 8 \[Pi] x + 4 x^2)])] + (3 \[Pi] - 2 x)^2 Sin[ 1/2 (\[Pi] - (\[Pi] x)/(\[Pi] - x) +  ArcCsc[(4 \[Pi] (\[Pi] - x) Csc[\[Pi]^2/(\[Pi] - x)])/( 5 \[Pi]^2 - 8 \[Pi] x + 4x^2)])];

x/.NSolve[f==0 &&  0<x<[Pi]]
math2021
  • 749
  • 3
  • 8

1 Answers1

1

Plotting f suggests that it has very many, if not an infinite number of zeros.

Plot[f, {x, 0, Pi}, PlotPoints -> 10000, ImageSize -> Large, 
    AxesLabel -> {x, "f"}, LabelStyle -> {15, Bold, Black}]

enter image description here

Plot[f, {x, 3, Pi}, PlotPoints -> 100000, ImageSize -> Large, 
    AxesLabel -> {x, "f"}, LabelStyle -> {15, Bold, Black}]

enter image description here

So, it is unlikely that all can be found, even with the powerful methods cited by Nasser. Some can be found with NSolve, however.

NSolveValues[f == 0 && 0 < x < Pi, x, Reals]
(* {1.5708, 1.5708, 2.35619, 2.61799, 2.74889, 2.82743, 2.87979, 
    2.91719, 3.10132, 3.11079, 3.12922, 3.13224, 3.14024} *)

NSolveValues[f == 0 && 3 < x < Pi, x, Reals]
(* {3.13105, 3.13267, 3.13291, 3.13306, 3.13473, 3.13485, 3.13515, 
    3.13648, 3.13735, 3.13767, 3.13816, 3.1397, 3.14003, 3.14034, 3.1412, 
    3.14142, 3.14148} *)

Be sure to specify that only Real roots are sought to speed the computation.

bbgodfrey
  • 61,439
  • 17
  • 89
  • 156
  • Thanks, the problem is that it can be easily checked that all the roots these methods give are rational multiples of $\pi$. x={1/2, 3/4, 5/6, 7/8, 9/10, 11/12, 13/14, 15/16, 17/18, 19/20, 21/ 22} \[Pi] , on the other hand, if you check the function at these values, you see that the function is not defined at all at these values since at these values, the argument of $\csc \left(\frac{\pi ^2}{\pi -x}\right)$ will be integer multiples of $\pi$. @bbgodfrey – math2021 Oct 02 '21 at 17:49
  • So, does this mean that Mathematica is providing the roots that the function is not defined at those values? These points are also visible in the plots. @bbgodfrey – math2021 Oct 02 '21 at 17:49
  • @math2021 NSolve is seeking values of x for which f is approximately, not exactly, equal to zero. Incidentally, Simplify[f /. x -> (2 n - 1) Pi/(2 n), n > 1 && n \[Element] Integers] spits out several error messages but finally yields 0. Probably, when it encounters an error, it tries a different order of simplification. – bbgodfrey Oct 02 '21 at 18:38