3D FEM Mesh - Accessing values of individual boundary elements

Question

I have 3D mesh and calculate the heat equation using NDSolve. I want to access the temperature values on the individual boundary elements to solve another problem (posted here).

I wrote some code that allows me to access the temperature from the interpolatingFunction from NDSolve on the individual boundary elements using an FVM approach (triangle element and it's centroid). I tested this approach by manually integrating over a boundary, but the solution differs too much from integrating using NIntegrate.

I think the error comes from FEM calculating on the nodes, rather than using the centroid. Is there a way to access the value of the boundary nodes (from the interpolatingFunction) and some kind of area of the node as a weight for integration?

A solution would be to calculate both integrals (manually and using NIntegrate) and calculate a correction factor that I can multiply with when using the individual values.

Find my approach below.

I am generating a mesh:

Needs["NDSolve`FEM`"]
xmax = 2;
ymax = 1;
zmax = 1;
cubi = Cuboid[{0, 0, 0}, {xmax, ymax, zmax}];
mesh = DiscretizeRegion[cubi, MaxCellMeasure -> 0.0001];
bmesh = ToBoundaryMesh[mesh]
Graphics3D[mesh, Axes -> True, AxesLabel -> {"x", "y", "z"}]

Gathering the required information from the boundary mesh:

triList =  bmesh["BoundaryElements"][[1, 1]];
coordsList = bmesh["Coordinates"];

Creating a list of all the triangles that I am interested in (here all the ones on the side of the cube where y==0, see this post if you want to use boundary markers to do so):

y0Tris = {}; (*List of all tris with y=0*)
(Find all triangle elements with all point's y coordinate = 0)
Do[
 currTri = triList[[i]];
yp1 = coordsList[[currTri[[1]]]][[2]];
 yp2 = coordsList[[currTri[[2]]]][[2]];
 yp3 = coordsList[[currTri[[3]]]][[2]];
If[yp1 == 0 && yp2 == 0 && yp3 == 0, AppendTo[y0Tris, currTri]]
, {i, Length[triList]}
 ]

Calculating the areas of the relevant triangles:

y0TrisAreas = Table[
   Area[Triangle[
     {coordsList[[currTri[[1]]]],
      coordsList[[currTri[[2]]]],
      coordsList[[currTri[[3]]]]}
     ]]
   , {currTri, y0Tris}];

Calculating the centroids of the relevant triangles:

y0TrisCentroids = Table[
   RegionCentroid[Triangle[
     {coordsList[[currTri[[1]]]],
      coordsList[[currTri[[2]]]],
      coordsList[[currTri[[3]]]]}
     ]]
   , {currTri, y0Tris}];

Now I calculate the heat equation, setting a heat flux on the left and a temperature on the right:

ks = 1;
(*solve heat equation*)
TFun = NDSolveValue[{ks*\!\(\*SubsuperscriptBox[\(\[Del]\), \({x, y, z}\), \(2\)]\(T[x, y, z]\)\) == 0
      + NeumannValue[-100, x == 0], 
      DirichletCondition[T[x, y, z] == 0, x == xmax]},
   T, {x, y, z} \[Element] mesh];

Integrating over the boundary y==0, calculating the integral of the temperature and the average temperature:

areaBoundary = NIntegrate[Piecewise[{{1, y == 0}, {0, True}}], {x, y, z} \[Element] bmesh];
timeInt = First@Timing[
    integTemp = NIntegrate[
      Piecewise[{{TFun[x, y, z], y == 0}, {0, True}}], {x, y, z} [Element] bmesh];(integrating over whole area T(x,y,z)dA)
    averageTemp = integTemp/areaBoundary; (calculating average temperature on boundary)
    ];
Print["Integrating time: " <> ToString@timeInt];
Print["Tavg*A: " <> ToString@integTemp];
Print["Tavg: " <> ToString@averageTemp];
Integrating time: 0.640625
Tavg*A: 200.
Tavg: 100.

And finally integrating manually by accessing the value of the temperature for each triangle element at it's centroid, multiplying with it's area and summing up over all triangles:

timeIntMan = First@Timing[
    (*performing manual integration*)
    integTempManual = Plus @@ Table[
       xcoord = y0TrisCentroids[[i]][[1]];
       ycoord = y0TrisCentroids[[i]][[2]];
       zcoord = y0TrisCentroids[[i]][[3]];
       TFun[xcoord, ycoord, zcoord]*
        y0TrisAreas[[i]](*calculating for each triangle T(centroid)*area_triangle*)
       , {i,Length[y0TrisCentroids]}];(*integrating over whole are T(x,y,z)dA*)
averageTempManual = integTempManual/areaBoundary;(*calculating average temperature on boundary*)
];

Print["Integrating manual time: " <> ToString@timeIntMan];
Print["Tavg*A: " <> ToString@integTempManual];
Print["Tavg: " <> ToString@averageTempManual];
Integrating manual time: 0.03125
Tavg*A: 200.
Tavg: 100.

Now this works fine for this simple case. I set up a case that is a bit more complex. Heat flux on the left like the prior example, but temperature dependent Neumann BC on the front (y==0)

ks = 1;
Tamb = 20;
alphaFreeConvection = 5;
TFun2 = NDSolveValue[{ks*!(*SubsuperscriptBox[([Del]), ({x, y, z}), (2)](T[x, y, z])) == 0
      + NeumannValue[-100, x == 0]
      + NeumannValue[(T[x, y, z] - Tamb)*alphaFreeConvection, y == 0]},
   T, {x, y, z} [Element] mesh];

Performing the integration as above gives different results. Note, that the difference between the approaches becomes far more significant for more complex cases.

Integrating time: 0.640625
Tavg*A: 60.
Tavg: 30.
Integrating manual time: 0.03125
Tavg*A: 59.9901
Tavg: 29.9951

What I want to use this for, is calculating the temperature of the boundary (y==0, x-z-plane) as a function of x. Therefore I would take all the individual temperatures of the boundary elements, associate them to their x-coordinate (here centroid of the triangle) and throw them it into an interpolation function.

EDIT - using the function @Oleksii Semenov propsed:

I tried calculating the temperature at the centroids of the triangles using barycentric coordinates to interpolate from the values on the nodes.

This approach isn't succsessful either.

Find the code of the approach below:

timeIntMan2Bary = First@Timing[
TemprArray = TFun2["ValuesOnGrid"];(get values of boundary nodes)
(loop over each triangle and sum up)
   integTempManual2Bary = Plus @@ Table[
      currTri = y0Tris[[i]];
  (*creating 2d coordinates for barycentric coordinates, 
  deleting y coordinate,
  would need to map 3d triangles to 2d if using more complex boundaries*)
  pLis = {
    Delete[coordsList[[currTri]][[1]], 2],
    Delete[coordsList[[currTri]][[2]], 2],
    Delete[coordsList[[currTri]][[3]], 2]
    };

  (*calculating centroid in 2d triangle coordinates, deleting y*)
  centroid = Delete[
    y0TrisCentroids[[i]]
    , 2];

  baryWeights = 
   ResourceFunction["BarycentricCoordinates"][pLis, 
    centroid];(*barycentric weights*)
  nodeVals =Flatten@Partition[TemprArray[[Flatten[currTri]]], 
     3];(*temperatures at nodes, triangle corners*)

  tempInterp = 
   Plus @@ (nodeVals*
      baryWeights);(*interpolate temperature from barycentric weights*)
  tempInteg = tempInterp*y0TrisAreas[[i]];

  tempInteg(*to table*)

  , {i, Length[y0Tris]}
  ];(*end table*)

];(end timing)
averageTempManual2Bary = integTempManual2Bary/
  NIntegrate[Piecewise[{{1, y == 0}, {0, True}}], {x, y, z} [Element] bmesh];
Print["Integrating manualBary time: " <> ToString@timeIntMan2Bary];
Print["Tavg*A: " <> ToString@integTempManual2Bary];
Print["Tavg: " <> ToString@averageTempManual2Bary];
Integrating manualBary time: 0.734375
Tavg*A: 60.1539
Tavg: 30.0769

EDIT - As @user21 mentioned, it seems to be unclear, what I want to do. Now I want to try explaining with equations.

I want to turn the temperature of the boundary of the solid (y=0) into a function of the x coordinate.

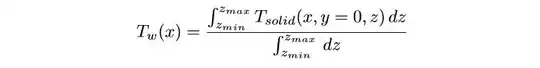
To do so, I was thinking to divide my x range into small segments and do the following. Thats why I want to use the node/triangle element values of the temperature to stuff them into the segments.

With this I would have T_w for discrete x coordinates. Those I could use to generate an interpolation function or else.

With this I want to solve the coupling of a 1D region with a 3D region. The problem is to match the heat going into the channel with the heat going out of the wall. Where alpha is the heat transfer coefficient and Pi*D_c is the circumference of the channel.

Answer 1

You can get solution values in nodes by

TemprArray = TFun[[4]]
{200., 200., 200., 200., 200., 200., 200., 200., 200., 200., 200., 

, 124.242, 127.273, 127.273, 130.303, 130.303, 130.303, 

124.242, 123.794, 133.333, 136.364}

It works in the case of stationary solution. For transient solutions there is another way.

As expected the number of mesh nodes coincide with length of TemprArray

Length[ToElementMesh[mesh]["Coordinates"]]
Length[TemprArray]
58134
58134

Further we can get temperature values for every triangle posed on surface y=0 by

Partition[TemprArray[[Flatten[y0Tris]]], 3]  

Calculation of $T_w(x)$

Lets introduce additional 1D mesh on $0\leq x\leq x_{max}$ and calculate average (averaging along $0\leq z\leq z_{max}$) values of surface temperature in nodes of this mesh. By using Interpolation we can obtain function $T_w(x)$

n = 10;               (*number of elements in x-direction*)
h = xmax/n;           (*spetial step size*)  
Xmesh = Table[(i - 1)*h, {i, 1, n + 1}];
Tw[x_] := NIntegrate[TFun[x, 0, z], {z, 0, zmax}]/zmax
TwP = Map[Tw, Xmesh];
TwInt = Interpolation[Transpose[{Xmesh, TwP}]]
pic = Plot[TwInt[x], {x, 0, xmax}, ImageSize -> 300, 
  AxesLabel -> {"x", "Tw"}]