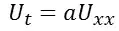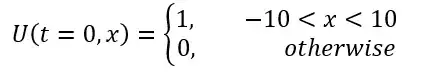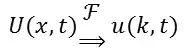How can I use fast Fourier transform (FFT) to solve a PDE (heat equation)?

Question

I'm trying to solve a one-dimensional heat equation (PDE) with the Fourier transform numerically, in the way it was done here. The equation:

,

is subject to the initial condition:

,

where U(x,t) is temperature, x is space, a is heat conductivity, and t is time.

I want to solve this equation using fast Fourier transform (FFT).

.

The key observation here is concerning the derivatives:

,

where k=2 pi/L[-N/2,N/2] is a spatial frequency or wave number. So, u(k,t) is a vector of Fourier coefficients and k square is a vector of frequency, so that

gives n decoupled ODEs, one for each these kj.

The respective code is:

   n = 1000;(*Number of discretization points*)
    L = 100; (*Length of domain**)
    T = 20; (*Time Integration*)
    a = 1; (*thermal diffusivity constant*)
    k = (2 Pi)/L Table[i, {i, -n/2, n/2 - 1}];(*define discrete wave number*)
    kt = Fourier[k];(*Re-order FFT wave number*)
    ic1 = Table[If[400 < i < 600, 1, 0], {i, Length[k]}]; (*initial condition*)
    ict = Fourier[ic1];(*Fourier Transform of initial condition*)
    ic = Table[Subscript[u, i][0] == ict[[i]], {i,Length[k]}];(*vector of initial condition in Fourier transform domain*)
    vars = Table[Subscript[u, i][t], {i, Length[k]}]; (*vector of variables*)
    eqns = Table[{Subscript[u, i]'[t] == -a (kt[[i]])^2 Subscript[u, i][t]}, {i,Length[k]}];(*model of ODEs system*)
    eqn = Join[eqns, ic];
    sol = NDSolve[eqn,vars, {t, 0, T}];(*Simulate in Fourier frequency domain*)

This error message appears:

General::munfl: (-1.4792510^-23+4.7229210^-303> I)+(1.5440710^-23-4.7229110^-303 I) is too small to represent as a> normalized machine number; precision may be lost. General::stop:

Further output of General::munfl will be suppressed during this > calculation.

How can I fix this?

Next, I intend to plot the solution by applying the inverse Fourier transform (IFFT).

s = Table[  Table[Evaluate[Subscript[u, j][t] /. sol], {t, 0, T}], {j,Length[k]}];(*select the solution of temperature in frequency domain*)
sin = InverseFourier[s];(*IFFT to return to spatial domain*)
fin = Table[{i, j, sin[[j, i, 1]]}, {i, Length[sin[[1]]]}, {j,Length[sin]}];
Table[ListPlot3D[fin[[i]]], {i, Length[fin]}];

The plot of the solution I'm looking for should be something like:

Answer 1

There are three mistakes here, mainly related to FFT.

First, you misunderstood the meaning of fftshift in the MATLAB code. It's not Fourier, but a shift. This has been discussed detailedly in the following post:

What's the correct way to shift zero frequency to the center of a Fourier Transform?

So we need to modify

kt = Fourier[k];

to

kt = fftshift@k;

Please find the definition of fftshift in the post linked above.

The next mistake lies in inverse FFT. You've typed

sin = InverseFourier[s];

which leads to a 2D (to be precise, 3D, because you haven't yet stripped out the redundant {} in this step) inverse FFT, but we actually only need a bunch of 1D inverse FFT in $k$ direction! So the line should be modified to

sin = InverseFourier /@ Transpose@s;

Finally, visualization. ListPlot3D isn't the correct tool for the expected plot. You need the new-in-12.3 ListLinePlot3D:

ListLinePlot3D@Transpose@fin

---

Just for fun, the following is a simplification for OP's code:

n = 1000;
L = 100;
T = 20;
a = 1;
k = 2 π/L Table[i - Floor[n/2], {i, 0, n - 1}];
(* Definition of fftshift isn't included in this post,
   please find it in the link above. *)
kt = fftshift[k];
ic1 = Table[If[-10 < x < 10, 1, 0], {x, -L/2, L/2, L/(n - 1)}];
ict = Fourier[ic1];
U[t_] = Table[u[i][t], {i, n}];
ic = U[0] == ict;
eqns = U'[t] == -a kt^2 U[t];
sollst = NDSolveValue[{eqns, ic}, U[t], {t, 0, T}]; // AbsoluteTiming
lst = Table[sollst, {t, 0, T}];
lstinverse = InverseFourier /@ lst;
domain = {{0, T}, {-1, 1} L/2};
ListLinePlot3D[lstinverse, DataRange -> Reverse@domain]

If you're not yet in v12.3 or later, the standard way the visualize the solution is to build an InterpolatingFunction first and plot then:

func = ListInterpolation[lstinverse, domain]
ParametricPlot3D[
 Table[{x, t, Re@func[t, x]}, {t, 1.2345, 19.2345}] // Evaluate, {x, -L/2, L/2}, 
 BoxRatios -> {1, 1, 0.4}]

Notice I've added a Re to remove the tiny imaginary part of the solution. (We don't need it in ListLinePlot3D because ListLinePlot3D is so clever that the tiny imaginary part is automatically removed. )

Answer 2

I would not use a numerical method if the problem can easily be solved analytically:

 sol[u_, t_] = 
 u[x, t] /. DSolve[{D[u[x, t], t] == D[u[x, t], {x, 2}], 
     u[x, 0] == If[Abs[x] < 10, 1, 0]}, 
    u, {x, -10, 10}, {t, 0, 20}][[1]]

The result can be plotted:

Plot3D[sol[x, t], {x, -30, 30}, {t, 0, 20}]