Is it possible to extract vertices and lines from this image of nonplanar graph?

Question

The recent post was particularly interesting (see Is it possible to extract vertices and lines from this image?), but I found was that method of the comments seemed unreliable when the graph was not plane graph. For example, we want to identify the figure below. The ones in bold are vertices of graph.

By halmir's way, we get following graph.

For another example,

I do not know whether there is a way for graph containing cross point.

Answer 1

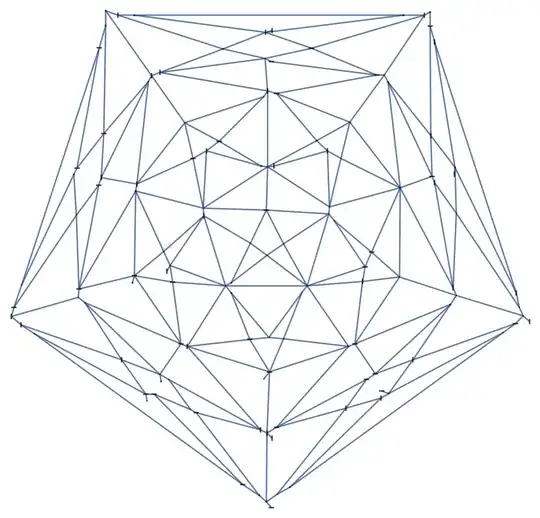
I'll start from the code given by flinty in the comment in order not to do this work again. Let us name his end result as firstStage:

img = Import["https://i.stack.imgur.com/ujHq1.png"];
vtxmask = Closing[Binarize@img, 2];
edgemask = Binarize@ImageMultiply[ColorNegate@img, vtxmask];
firstStage = 
 Pruning@Thinning@
   ImageAdd[edgemask, ImageMultiply[ColorNegate@vtxmask, Red]]

The rest is mine.

I'll proceed in the same manner as in my previous answer. Most of the code is self-describing, so I'll comment on it only a little.

nodesRemoved = Binarize[firstStage];
nodes = firstStage - nodesRemoved;
nodesLabeled = MorphologicalComponents[nodes]*1000000;
nodesLabeled // Colorize

After removing the nodes we have full edges with crossovers. We broke full edges at crossovers, and then separate broken edges and crossovers by labeling:

brokenEdges = 
  DeleteSmallComponents[
   MorphologicalTransform[nodesRemoved, 
    If[#[[2, 2]] == 1 && Total[#, 2] <= 3, 1, 0] &], 5];
brokenEdgesLabeled = MorphologicalComponents[brokenEdges]*100;
brokenEdgesLabeled // Colorize
crossovers = nodesRemoved - brokenEdges;
crossoversLabeled = MorphologicalComponents[crossovers];
crossoversLabeled // Colorize

Bringing back together nodes, crossovers, and broken edges (but now all they have distinct labels!):

everythingLabeled = 
  brokenEdgesLabeled + crossoversLabeled + nodesLabeled;
everythingLabeled // Colorize

Each crossover occurs at the intersection of two full edges and connects 4 line segments ("broken edges"):

crossoversWithBrokenEdges = 
  ComponentMeasurements[everythingLabeled, 
   "Neighbors", #Label < 100 &];

For determining pairs of line segments ("broken edges") that correspond to one full edge, we determine centroids of broken edges and crossovers:

crossoversCentroids = 
  ComponentMeasurements[everythingLabeled, "Centroid", #Label < 100 &];
brokenEdgesCentroids = 
  ComponentMeasurements[everythingLabeled, "Centroid", 
   100 <= #Label < 1000000 &];

Every broken edge connects a crossover and a node, every full edge connects two nodes:

brokenEdgesWithNodes = 
  ComponentMeasurements[everythingLabeled, "Neighbors", 
   100 <= #Label < 1000000 &];

Let us define a function that determines which pair of broken edges correspond to the full edge. The key idea is that planar angle composed by the centroids of two broken edges with centroid of the crossover inbetween should be near 180 degrees:

Clear[joinBrokenEdges]
joinBrokenEdges[cross_ -> labels : {p1_, p2_, p3_, p4_}] := 
  Module[{pts = labels /. brokenEdgesCentroids, 
    cr = cross /. crossoversCentroids, n, pair1, pair2},
   n = MaximalBy[# -> PlanarAngle[cr -> pts[[{1, #}]], "Interior"] & /@ {2, 3, 4}, 
      Last][[1, 1]];
   pair1 = labels[[{1, n}]]; 
   pair2 = labels[[Complement[{2, 3, 4}, {n}]]];
   Rule[Alternatives @@ #, #] & /@ {pair1, pair2}
   ];

With this function, we transform crossoversWithBrokenEdges into a set of rules for joining broken edges:

joiningRules = Flatten[joinBrokenEdges /@ crossoversWithBrokenEdges];

These rules apply only to really broken edges, so we can easily get full edges from brokenEdgesWithNodes:

fullEdgesWithNodes = 
  Cases[brokenEdgesWithNodes /. joiningRules, 
   HoldPattern[_Integer -> _]];

Joining broken edges is a bit trickier:

joinedEdgesWithNodes = 
  Normal[Select[Flatten[#], # >= 1000000 &] & /@ 
    GroupBy[Cases[brokenEdgesWithNodes /. joiningRules, 
      HoldPattern[_List -> _]], First -> Last]];

Now we have all edges recovered:

allEdges = 
  Join[fullEdgesWithNodes[[All, 2]], joinedEdgesWithNodes[[All, 2]]];

We also need node centroids in order to reproduce the original layout of the graph:

nodesCentroids = 
  ComponentMeasurements[everythingLabeled, 
   "Centroid", #Label >= 1000000 &];

Now everything is ready:

Graph[Style[UndirectedEdge @@ #, RandomColor[]] & /@ allEdges, 
 VertexCoordinates -> nodesCentroids, 
 VertexLabels -> Placed["Name", Tooltip], 
 EdgeLabels -> Placed["Name", Tooltip], VertexSize -> .2]

Answer 2

The problems in the first graph I've addressed in the comments.

This is what I've managed to do for the second graph. There is a fine tuning involved in the Closing filter radius and the threshold values. Once it finds the vertices, it works by thickening the image first (using an Erosion) then seeding random points along lines between pairs of points and taking the average pixel value along that line. If this value is above a threshold then it's likely there's an edge between that pair. It then deals with the situation that three points could be colinear. I assume that there are no ambiguous edges that go through three points and delete these spurious connections by removing edges that get too close to any third point:

img = ColorConvert[
   RemoveAlphaChannel@Import["https://i.stack.imgur.com/9gOG3.png"], 
   "Grayscale"];
(* Closing 5 and SpanningTree seemed to work the best here )
vtxmask = Closing[Binarize@img, 5];
vertexpixels = N@PixelValuePositions[vtxmask, 0];
clusters = FindClusters[vertexpixels, Method -> "SpanningTree"];
vtxpositions = Mean /@ clusters;
( Show the image with calculated vtxs overlaid *)
Show[img,
 Graphics[{Red, Point[vtxpositions]}]
 ]
(* the line test creates random points between two vertices. If the 
average pixel value at these n points 
is above some threshold, then they are probably connected *)
lerp[a_, b_, t_] := (1 - t) a + t b;
lineTest[pt1_, pt2_, img_, n_, threshold_] := With[{
   positions = lerp[pt1, pt2, #] & /@ RandomReal[1, n]
   }, Mean[PixelValue[img, positions]] > threshold
  ]
(* Note we need to thicken the image a bit and invert it so that 1 
corresponds to edges, and zero empty space *)
edges = With[{thickened = ColorNegate@Erosion[img, 1]},
   If[lineTest[#[[1]], #[[2]], thickened, 30, 0.9], 
      UndirectedEdge @@ #, Nothing] & /@ Subsets[vtxpositions, {2}]
   ];
(* At this point we have some edges which go through three points.
We assume the graph image is laid out well enough. 
If there are collinear vertices A,B,C, which have connections, 
we don't want to connect A and C, only A,B and B,C. 
Remove edges where there are three vtxs approx on the line *)
edgeFilter[edge_, vtxs_, threshold_] := 
 With[{rdf = RegionDistance[Line[edge /. UndirectedEdge -> List]]},
  Count[vtxs, v_ /; rdf[v] < threshold] < 3]
filtered = Select[edges, edgeFilter[#, vtxpositions, 20] &];
Graph[filtered, VertexCoordinates -> VertexList[filtered], 
 VertexSize -> Large]

This is by no means a good general method as it requires too much fine tuning, so expect it to generalize poorly to other non-planar graphs which will likely require human intervention.